Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Gọi S và \(l\) là tiết diện và chiều dài của thanh.
Trọng lượng của thanh là :
P=10.D.S.\(l\)
Khi thanh nằm cân bằng, phần thể tích nước dâng lên cũng chính là phần thể tích thanh chìm trong nước. Ta có :
V=\(S_0\Delta h\)
Lực đẩy Acsimét tác dụng vào thanh :
\(F_0=10.D_0.V=10.D_0S_0\Delta h\)
Do thanh cân bằng nên :
P=\(F_0\) hay \(10.D.S.l=10.D_0.S_0.\Delta h\)
=> \(l\) = \(\dfrac{D_0}{D}.\dfrac{S_0}{S}.\Delta h\)....(1)
Khi thanh chìm hoàn toàn trong nước, nước dâng lên một lượng bằng thể tích thanh. Gọi \(\Delta h\) là phần nước dâng lên lúc này, ta có :
S.\(l=S_0.\Delta h\)......(2)
Từ (1) và (2) suy ra :
\(\Delta H=\dfrac{D_0}{D}.\Delta h\)
Và chiều cao cột nước trong bình lúc này là :
H '= H+\(\Delta H\)
=H+\(\dfrac{D_0}{D}.\Delta h=20+\dfrac{1}{0,8}.4\)
H'=25cm.
Vậy.................................................
b) Khi thanh chìm hoàn toàn trong nước, lực tác dụng là :
F=\(F_1-P=10D_0Sl-10DSl\)
=\(10Sl\left(D_0-D\right)=10.50.10^{-6}\left(1-0,8\right)10^3\)
F=0,1N.
Bạn nên xem mấy cái câu hỏi tương tự ấy trước. Nếu không có rồi mới đăng câu hỏi lên bạn!:v Câu hỏi của Ha Dlvy - Vật lý lớp 8 | Học trực tuyến.
Khi thanh gỗ nổi nó dài: \(P=F_A\)
\(\Rightarrow10D_{gỗ}\cdot V_{gỗ}=10D_{nc}\cdot V_{nc}\)
\(\Rightarrow D_{gỗ}\cdot S\cdot h=D_{nc}\cdot S\cdot h_1\)
\(\Rightarrow h=\dfrac{D_{nc}}{D_{gỗ}}\cdot h_1=\dfrac{0,8}{1}\cdot20=16cm\)
Gọi H là chiều cao mực nước trong bình khi chưa thả gỗ.
Diện tích đáy bình:
\(S_{bình}=\pi\cdot R^2=\left(\dfrac{20}{2}\cdot10^{-2}\right)^2\cdot\pi=0,01\pi\left(m^2\right)\)
Diện tích thanh gỗ:
\(S_{gỗ}=\pi\cdot R^2=\left(\dfrac{10}{2}\cdot10^{-2}\right)^2\cdot\pi=0,0025\pi\left(m^2\right)\)
Giả sử \(V_1,V_2\) là thể tích bình khi chưa thả gỗ và đã thả gỗ.
\(\Rightarrow V_1=V_2-V_{chìm}=S_{bình}\cdot\left(h_1+h_2\right)-S_{gỗ}\cdot h_1\)
\(=0,01\pi\cdot\left(0,2+0,16\right)-0,0025\pi\cdot0,2=9,7\cdot10^{-3}m^3\)
\(H=\dfrac{V_{nc}}{S_{bình}}=\dfrac{9,7\cdot10^{-3}}{0,01\pi}=0,31m=31cm\)
a) Gọi tiết diện và chiều dài thanh S là S' và L. Ta có trọng lượng của thanh S là
P = 10.D2.S'.L
Thể tích nước dâng lên bằng thể tích phần thanh sắt chìm trong nước
V = ( S - S' ).h
Lực đẩy acsimet tác dụng lên thanh S
F1 = 10.D1.( S - S' ).h
Do thanh sắt ở trạng thái cân bằng nên P = F1
=> 10.D2.S'.L = 10.D1.( S - S' ).h
<=> L = [ D1/D2 ].[ ( S - S' )/S' ].h (*)
Khi thanh sắt bị nhấn chìm hoàn toàn trong nước thì thể tích nước dâng lên = thể tích thanh.
Gọi Vo là thể tích thanh sắt ta có Vo = S'.L
Thay (*) vào ta có
Vo = D1/D2.( S - S' ).h
Khi đó; mực nước dâng lên 1 đoạn ∆h so với khi chưa thả thanh sắt vào
∆h = Vo/( S - S' ) = D1/D2.h
=> Chiều cao cột nước khi nhúng hoàn toàn thanh sắt là
H' = H + ∆h = H + D1/D2.h
Thay D1 = 1g/cm³ và D2 = 0,8g/cm³ ( Tra bảng SGK lí 8 ) vào ta có
H' = 15 + 10 = 25
b) Lực tác dụng lên thanh đồng lúc nhấn chìm gồm P; Lực đẩy Acsimet F2; và lực đẩy F chìm xuống, do thanh sắt cân bằng nên ta có
F = F2 - P = 10.D1.Vo - 10.D2.S'.L
mà Vo = S'.L
=> F = 10.S'.L( D1 - D2 ) = 2.S'.L = 2.0,2.0,1 = 0,4 N
Từ (*) => S = [ ( D2/D1 )( L/h ) + 1 ].S' = 3.S' = 30 cm²
Do đó; khi thanh đi thêm vào nước 1 đoạn x thì ∆V = x.S' thì nước dâng thêm 1 đoạn:
y = ∆V/( S - S' ) = ∆V/2S' = x/2
Mặt khác, nước dâng thêm do với lúc đầu một đoạn
∆h - h = ( D1/D2 - 1 ).h = 2 cm
=> x/2 = 2 => x = 4
Vậy thanh đồng đã di chuyển được quãng đường dài x + x/2 = 4 => x = 8/3 cm
Và lực tác dụng tăng từ 0 → F = 0,4 N => công thực hiện là
A = 1/2.F.x = 1/2.0,4.8/3.10‾ ² = 5,33.10‾ ² J
a) Do thanh gỗ cân bằng trong nước nên trọng lượng cân bằng với lực đẩy Acsimét. Ta có :
10. \(10.D_1.S_2.h=10.D_2.S_2l\)
=> \(l=\dfrac{D_1}{D_2}h=\dfrac{1}{0,8}.20=25cm\)
Vậy \(l=25cm\)
b) Khi thả gỗ vào nước, phần nước dâng lên ứng với thể tích thanh gỗ chìm trong nước . Gọi ΔH là phần nước dâng lên, ta có :
\(S_2h=S_1\text{ Δ}H\)
=> \(\text{ Δ}H=\dfrac{S_2h}{S_1}=\dfrac{10.20}{30}=\dfrac{20}{3}=6,66cm\)
Gọi H, H' là chiều cao mực nước trước vào sau khi thả thanh gỗ vào , ta có :
H' = H + ΔH
Hay : H = H' - \(\text{ Δ}H=\left(h+\text{ Δ}h\right)-\text{ Δ}H\)
H = ( 20 + 2) - 6,66 = \(\dfrac{46}{3}=15,34cm\)
* Có thể tìm thể tích nước có trong bình :
\(V=S_1\text{Δ}h+\left(S_1-S_2\right)h\)
Hay chiều cao mực nước đã có trong bình lúc đầu :
\(H=\dfrac{V}{S_1}=\text{Δ}h+\dfrac{S_1-S_2}{S_1}h\)
H =15,33cm.
c) Nếu nhấn chìm hoàn toàn được thanh gỗ trong bình thì chiều cao tối thiểu mực nước trong bình lúc này là: \(l=25cm\)
=> Thể tích nước và gỗ là: \(V^'=30.25=750cm^3\)
=> Thể tích nước phải là: \(V_n=V^'-S_2.1=750-250=500cm^3\)
=> Không thể nhấn chìm hoàn toàn thanh gỗ được
[Vật lí 8] Box lí nâng cao cho mem hm | Diễn đàn HOCMAI - Cộng đồng học tập lớn nhất Việt Nam
vào mà xem
a) Gọi V,Vt lần lượt là thể tích phần ngập trong nước của thanh và thể tích thanh.
)
)
)
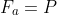
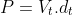
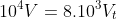
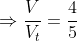
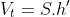
Khi thanh nằm cân bằng trên mặt chất lỏng:
Lại có:
Từ 1 và 2 ta có phương trình:
Ta có:
Vậy độ cao tính từ đáy lên là 25 cm