Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trong toán học, mỗi cách xếp thứ tự đá luân lưu của 5 cầu thủ được gọi là hoán vị.

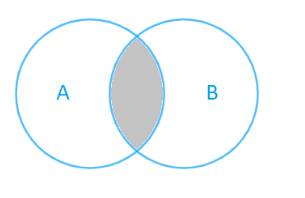
Phần màu xám là phần giao nhau giữa tập hợp A và tập hợp B: vừa thuộc A, vừa thuộc B.
Do đó phần màu xám là \(A \cap B\)
Chọn đáp án A

Gọi M là vị trí phát ra âm thanh cầu cứu trong rừng.
Gọi \({t_1},{t_2}\)lần lượt là thời gian trạm A, B nhận được tín hiệu cầu cứu (đơn vị: giây)
\( \Rightarrow {t_A} = {t_B} - 6 \Leftrightarrow {t_B} - {t_A} = 6\)
Đổi \(v = 1{\rm{ }}236{\rm{ }}km/h{\rm{ }} = \frac{{\;1236}}{{3600}}km/s = \frac{{103}}{{300}}km/s.\;\)
Ta có: \(MA = {t_A}.v;MB = {t_B}.v\)
\( \Rightarrow MB - MA = ({t_B} - {t_A}).v = 6.\frac{{103}}{{300}} = 2,06(km)\)
Như vậy, tập hợp các điểm M là một hypepol nhận A, B làm hai tiêu điểm.
Ta có: \(AB = 16 = 2c \Rightarrow c = 8\); \(\left| {MA - MB} \right| = 2,06 = 2a \Rightarrow a = 1,03\)
\( \Rightarrow {b^2} = {c^2} - {a^2} = {8^2} - 1,{03^2} = 62,9391\)
Vậy phương trình chính tắc của hypebol đó là: (H) \(\frac{{{x^2}}}{{1,0609}} - \frac{{{y^2}}}{{62,9391}} = 1\)
Do MA < MB nên M thuộc của nhánh (H) gần A.
Vậy phạm vi tìm kiếm vị trí phát ra âm thanh đó là nhánh gần A của hypebol (H) có phương trình \(\frac{{{x^2}}}{{1,0609}} - \frac{{{y^2}}}{{62,9391}} = 1\).

Tham khảo:
Gọi \(x\) là số bạn tham gia thi đấu cả bóng đá và cầu lông.
Ta có: 16 bạn thi đấu bóng đá và 11 bạn thi đấu cầu lông
\( \Rightarrow \) Có \(16 - x\) bạn chỉ tham gia thi đấu bóng đá mà không thi đấu cầu lông.
Và có \(11 - x\) bạn chỉ tham gia thi đấu cầu lông mà không thi đấu bóng đá.
Ta có biểu đồ Ven như sau:
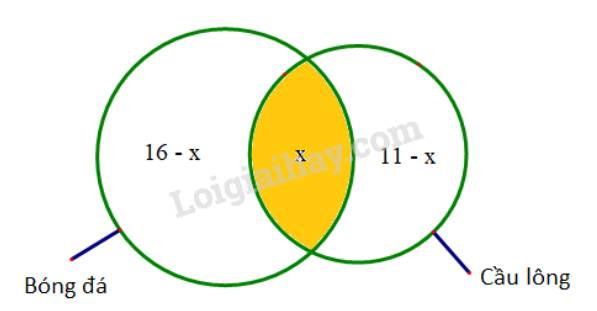
Tổng số bạn tham gia thi đấu bóng đá và cầu lông là: 16-x + x + 11-x = 24 => x=3.
Vậy lớp 10A có 3 bạn tham ggia thi đấu cả bóng đá và cầu lông.


a) Tập hợp E gồm những ứng viên đạt yêu cầu về chuyên môn nhưng không đạt yêu cầu về ngoại ngữ là: \(E = \{ {a_2};{a_7}\} \)
b) Xác định tập hợp F gồm những ứng viên không đạt yêu cầu về chuyên môn là: \(F = \{ {a_3};{a_4};{a_9}\} \)

Gọi \(y = f(x) = a{x^2} + bx + c\) là công thức của hàm số có đồ thị là hình ảnh của bộ phận chống đỡ.
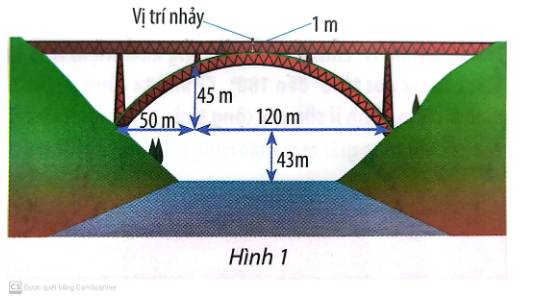
Chọn hệ trục tọa độ Oxy như hình dưới:
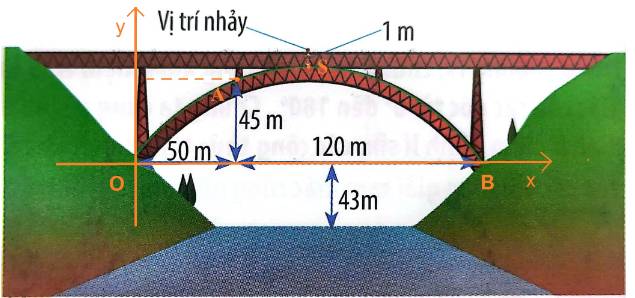
Gọi S là đỉnh của parabol, dưới vị trí nhảy 1m.
A, B là các điểm như hình vẽ.
Dễ thấy: A (50; 45) và B (120+50; 0) = (170; 0).
Các điểm O, A, B đều thuộc đồ thị hàm số.
Do đó:
\(f(0) = a{.0^2} + b.0 + c = 0 \Leftrightarrow c = 0\)
\(f(50) = a{.50^2} + b.50 + c = 45 \Leftrightarrow a{.50^2} + b.50 = 45\)
\(f(170) = a{.170^2} + b.170 + c = 0 \Leftrightarrow a{.170^2} + b.170 = 0 \Leftrightarrow a.170+ b = 0\)
Giải hệ phương trình \(\left\{ \begin{array}{l}a{.50^2} + b.50 = 45\\a.170 + b = 0\end{array} \right.\) ta được \(a = - \frac{{3}}{{400}};b = \frac{{51}}{{40}}\)
Vậy \(y = f(x) = - \frac{{3}}{{400}}{x^2} + \frac{{51}}{{40}}x\)
Đỉnh S có tọa độ là \({x_S} = \frac{{ - b}}{{2a}} = \frac{{ - \frac{{51}}{{40}}}}{{2.\left( { - \frac{{3}}{{400}}} \right)}} = 85;\;{y_S} = - \frac{{3}}{{400}}.8{5^2} + \frac{{51}}{{40}}.85 = \frac{{867}}{{16}} \approx 54,2\)
Khoảng cách từ vị trí bắt đầu nhảy đến mặt nước là: \(1 + 54,2 + 43 = 98,2(m)\)
Vậy chiều dài của sợi dây đó là: \(98,2:3 \approx 32,7\,(m)\)

Gọi \(X\) là tập hợp các học sinh trong lớp, \(A,B\) lần lượt là tập hợp các học sinh đăng kí chơi cầu lông và chơi bóng bàn.
Như vậy tập hợp học sinh đăng kí chơi cả hai môn là \(A\cap B\). Tập hợp học sinh đăng kí ít nhất một môn là \(A\cup B\)
Ta có \(N\left(A\cup B\right)=50-10=40\)
\(a,\) Ta có \(N\left(A\cup B\right)=N\left(A\right)+N\left(B\right)-N\left(A\cap B\right)\)
\(\Rightarrow N\left(A\cap B\right)=\left(A\right)+N\left(B\right)-N\left(A\cup B\right)=30+28-40=18\)
Vậy có \(18\) học sinh đăng kí chơi cả hai môn
\(b,\) Số học sinh chỉ đăng kí chơi một môn là
\(N\left(A\cup B\right)-N\left(A\cap B\right)=40-18=22\)

 Yêu cầu chứng minh
Yêu cầu chứng minh y nha mn :)))) cái kia sợ k thấy
y nha mn :)))) cái kia sợ k thấy
a)
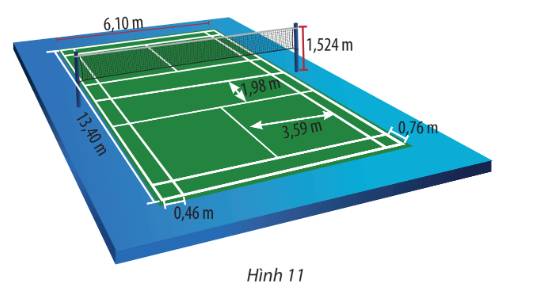
Chọn hệ trục tọa độ như Hình 9 (vị trí rơi của cầu thuộc trục hoành và vị trí cầu rời mặt vợt thuộc trục tung).
Với \(g = 9,8\;m/{s^2}\), góc phát cầu \(\alpha = {30^o}\), vận tốc ban đầu \({v_0} = 12\;m/s\), phương trình quỹ đạo của cầu là:
\(y = \frac{{ - 9,8}}{{{{2.12}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7 = - \frac{{4,9}}{{108}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7\)
Vị trí cầu rơi chạm đất là giao điểm của parabol và trục hoành nên giải phương trình \( - \frac{{4,9}}{{108}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 0,7 = 0\) ta được \({x_1} \approx - 1,11\) và \({x_2} \approx 13,84\)
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 13,84 m > 13,4 m (chiều dài cả sân)
Vậy lần phát cầu đã bị hỏng vì điểm rơi của cầu nằm ngoài đường biên ngoài.
b)
Ta so sánh tung độ của điểm trên quỹ đạo (có hoành động bằng khoảng cách từ điểm phát cầu đến chân lưới phân cách) với chiều cao mép trên của lưới.
Với \(g = 9,8\;m/{s^2}\), góc phát cầu \(\alpha = {30^o}\), vận tốc ban đầu \({v_0} = 8\;m/s\), vị trí phát cầu cách mặt đất 1,3 m. Phương trình quỹ đạo của cầu là:
\(y = \frac{{ - 9,8}}{{{{2.8}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3 = - \frac{{4,9}}{{48}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3\)
Khi \(x = 4,\)ta có \(y = - \frac{{4,9}}{{48}}{.4^2} + \frac{{\sqrt 3 }}{3}.4 + 1,3 \approx 1,98 > 1,524\)
Vậy quỹ đạo của cầu cao hơn mép trên của lưới.
Tiếp theo ta kiểm tra vị trí cầu rơi có vượt đường biên ngoài hoặc chưa tới đường biên trong hay không.
Vị trí cầu rơi chạm đất là giao điểm của parabol và trục hoành nên giải phương trình \(y = \frac{{ - 9,8}}{{{{2.8}^2}.{{\left( {\frac{{\sqrt 3 }}{2}} \right)}^2}}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3 = - \frac{{4,9}}{{48}}{x^2} + \frac{{\sqrt 3 }}{3}.x + 1,3\) ta được \({x_1} \approx - 1,73\) và \({x_2} \approx 7,38\)
Giá trị nghiệm dương cho ta khoảng cách từ vị trí người chơi cầu lông đến vị trí cầu rơi chạm đất là 7.38 m.
Dễ thấy: độ dài h (chiều dài của khu vực hợp lệ) là: \(13,4:2 - 1,98 -0,76= 3,96\) (m).
Do đó lần phát là hợp lệ nếu khoảng cách từ vị trí phát đến điểm rơi thuộc khoảng \(4 + 1,98 = 5,98(m)\) và \(4 + 1,98 +3,96= 9,94(m)\) và \(5,98 < 7,38 < 9,94\).
Như vậy vị trí quả cầu trên mặt đất nằm giữa đường biên trong và đường biên ngoài.
Kết luận: lần phát cầu này được coi là hợp lệ.