Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Độ cao các thửa ruộng so với mực nước biển tạo thành một cấp số cộng với số hạng đầu u1 = 1 250 m và công sai d = 1,2 (m).
Khi đó công thức tổng quát của cấp số cộng là: un = u1 + (n – 1).d = 1 250 + (n – 1).1,2.
Vậy độ cao của thửa ruộng thứ 10 so với mực nước biển là:
u10 = 1 250 + (10 – 1).1,2 = 1 260,8 m.

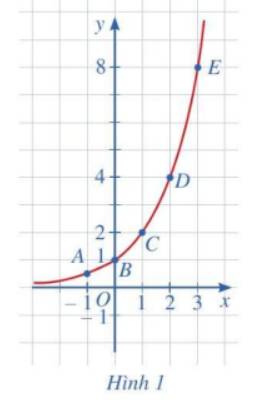
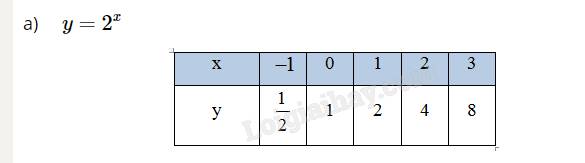
a:
| x | -1 | 0 | 1 | 2 | 3 |
| y | \(\dfrac{1}{2}\) | 1 | 2 | 4 | 8 |
b: Tham khảo:
c: Tọa độ giao điểm của hàm số với trục tung là B(0;1)
Đồ thị hàm số này ko cắt trục hoành
d:
\(\lim\limits_{x\rightarrow+\infty}2^x=+\infty;\lim\limits_{x\rightarrow-\infty}2^x=+\infty\)
=>Hàm số này đồng biến trên R
Bảng biến thiên:


a) \(y = {\left( {\frac{1}{2}} \right)^x}\)

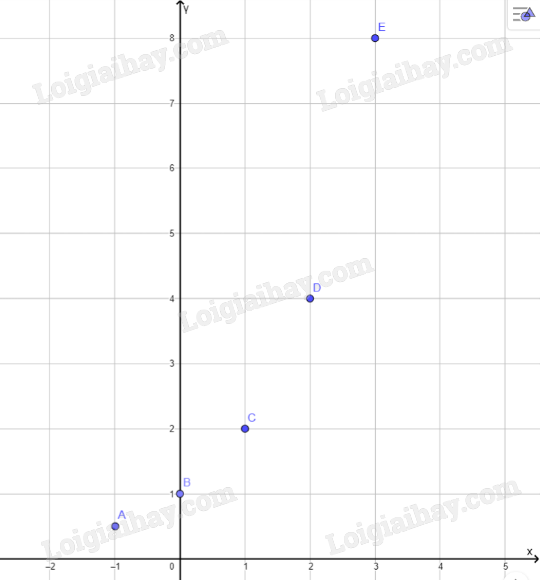
a) Biểu diễn các điểm ở câu a:
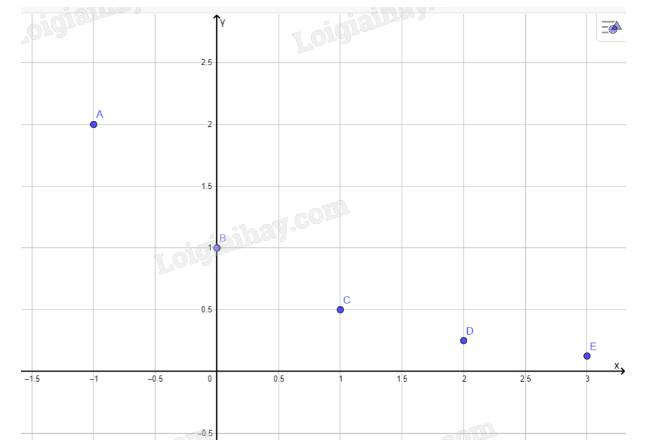
b) Tọa độ giao điểm của đồ thị hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) với trục tung là (0;1)
Đồ thị hàm số đó không cắt trục hoành
c) \(\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{1}{2}} \right)^x} = 0;\,\,\mathop {\lim }\limits_{x \to - \infty } {\left( {\frac{1}{2}} \right)^x} = + \infty \)
Hàm số \(y = {\left( {\frac{1}{2}} \right)^x}\) nghịch biến trên toàn \(\mathbb{R}\)
Bảng biến thiên của hàm số:


Số thành viên nữ của tố `23` là: `60. 5/12=25` (thành viên)
`=>` Số thành viên nam của tổ `23` là: `60-25=35` (thành viên)
`@TH1:` Chọn `3` giáo viên mà không có tổ trưởng
`=>` Có `C_25 ^2 .C_33^1 +C_25 ^1 .C_33^2=23100` cách
`@TH2:` Chọn `3` thành viên trong đó có `1` tổ trưởng là `1` trong `2` tổ trưởng nam.
`=>` Có `2.C_25 ^2=600` cách
`@TH3:` Chọn `3` thành viên trong đó có cả `2` tổ trưởng
`=>` Có `1.C_25 ^1=25` cách
`=>` Có tất cả `23100+600+25=23725` cách
`->bb B`

Đáp án B
Đặt t = 3sin x - 4 cos x => -5 ≤ t ≤ 5
Ta có: y = t2 – 2t + 2m – 1 = (t – 1)2 + 2m - 2
Với mọi t ta có (t – 1)2 ≥ 0 nên y ≥ 2m - 2 => min y = 2m - 2
Hàm số chỉ nhận giá trị dương ⇔ y > 0 ∀x ∈ R ⇔ min y > 0
⇔ 2m - 2 > 0 ⇔ m > 1


Khi bể nước có đáy thuộc mặt phẳng nằm ngang, thì mặt nước nằm trong mặt phẳng song song với đáy. Vì vậy, để đo độ sâu của bể, ta có thể đo khoảng cách từ mặt nước đến đáy bể.
Khi thả quả dọi vào bể nước, nó sẽ chìm dưới mặt nước và chạm đến đáy bể. Khi kéo quả dọi lên, ta sẽ thấy một đoạn dây dọi nằm trong bể nước và một đoạn dây dọi ở ngoài bể nước. Đoạn dây dọi nằm trong bể nước có độ dài bằng khoảng cách từ mặt nước đến chỗ quả dọi chạm đáy bể. Do đó, để đo độ sâu của bể, ta chỉ cần đo độ dài của đoạn dây dọi nằm trong bể nước.
Công thức để tính độ sâu của bể nước sẽ là:
Độ sâu bể = chiều dài của đoạn dây dọi nằm trong bể nước

a) Điểm G là điểm biểu diễn cho góc lượng giác có số đo \(\alpha \). Khi đó tọa độ điểm \(G\left( {3cos\alpha ;{\rm{ }}3sin\alpha } \right)\).
Chiều cao của gàu ở vị trí G đến mặt nước là: \(3{\rm{ }} + {\rm{ }}3sin\alpha \) (m).
b) Khoảng cách của gàu đến mặt nước bằng 1,5m khi \(3 + 3sin\alpha = 1,5 \Leftrightarrow sin\alpha {\rm{ }} = \frac{{ - 1}}{2}\)
Một vòng quay là 30 giây và t nằm trong khoảng từ 0 đến 1 phút do đó t ∈ [0; 2π].

Theo đề bài ta có dãy số chỉ độ cao của quả bóng là một cấp số nhân có số hạng đầu \({u_1} = 120\) và công bội \(q = \frac{1}{2}\).
Tổng các độ cao của quả bóng sau 10 lần rơi đầu tiên là:
\({S_{10}} = \frac{{{u_1}\left( {1 - {q^{10}}} \right)}}{{1 - q}} = \frac{{120\left( {1 - {{\left( {\frac{1}{2}} \right)}^{10}}} \right)}}{{1 - \left( {\frac{1}{2}} \right)}} = 239,765625\left( {cm} \right)\).







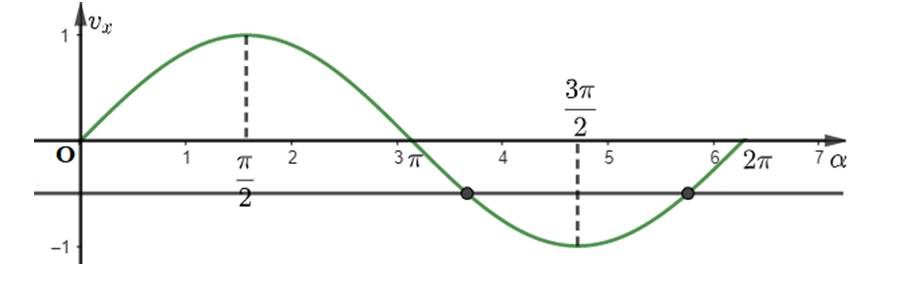
Để ống đựng nước cách mặt nước 2m thì \(h = \left| y \right| = 2\)
Hay \(\left| {2,5.\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2} \right| = 2\)
Suy ra \(2,5.\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2 = 2\) hoặc \(2,5.\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2 = - 2\)
*) \(2,5.\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2 = 2\\ \Leftrightarrow \sin \left( {2\pi x - \frac{\pi }{2}} \right) = 0\\ \Leftrightarrow 2\pi x - \frac{\pi }{2} = k\pi ,k \in Z\\ \Leftrightarrow 2x - \frac{1}{2} = k,k \in Z\\ \Leftrightarrow x = \frac{{2k + 1}}{4},k \in Z\\ \Leftrightarrow x \in \left\{ {....; - \frac{1}{4};\frac{1}{4};\frac{3}{4};....} \right\}\)
*)\(2,5.\sin \left( {2\pi x - \frac{\pi }{2}} \right) + 2 = - 2\\ \Leftrightarrow \sin \left( {2\pi x - \frac{\pi }{2}} \right) = - 1,6\, < - 1\)
Vì tập giá trị của hàm số sin là \(\left[ { - 1;1} \right]\) nên trong trường hợp này phương trình vô nghiệm.