Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách 2:
Gọi x là số dãy ghế lúc đầu (Đk:x và x là ước của 250, dãy)
Số chỗ ngồi ở mỗi dãy lúc đầu: 250/x (chỗ)
Số dãy ghế lúc sau là x + 3 (dãy). Số chỗ ngồi lúc sau: 308/(x+3) (chỗ).
Vì mỗi dãy ghế phải kê thêm 1 chỗ ngồi nữa thì vừa đủ ta có PT:
308/(x+3)-250/x=1↔x^2-55x+750=0↔[█(x_1=30 (loại) vì 250 không chia hết cho 30@x_2=25 (nhận))┤
Vậy lúc đầu có 25 dãy ghế. Mỗi dãy ghế có 10 chỗ ngồi.
Cách 1:
Gọi x là số dãy ghế lúc đầu; y là số người trên mỗi dãy ghế lúc đầu (x,y>0)
Ta có tổng cộng 250 người nên x.y =250 (1)
Nếu thêm 3 dãy ghế tức x + 3 thì mỗi dãy còn lại phải xếp thêm 1 người tức y + 1
Ta có: (x+3).(y+1) = 250 (2)
Từ (1) và (2) ta có hệ:
Vậy lúc đầu có 25 dãy ghế. Mỗi dãy ghế có 10 chỗ ngồi.

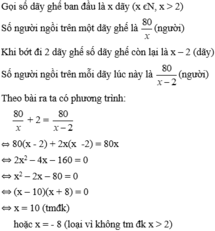
Vậy số dãy ghế ban đầu là 10 dãy và số người ngồi trên 1 dãy là 8 người.

gọi số dãy ghế là x
theo đề bài ta có phương trình (x+2)*(100/x+2)=144
giải ra ta được x=10

Gọi x là số dãy ghế; y là số người trên mỗi dãy ghế (x,y>0)
Ta có tổng cộng 80 người nên x*y =80 <=> x =80/y (1)
Nếu bớt đi 2 dãy ghế tức x-2 thì mỗi dãy còn lại phải xếp thêm 2 người tức y+2
Ta có: (x-2)*(y+2) = 80 (2)
Thay (1) vào (2) ta có: 2y^2 +4y -160 =0
<=> y=8 => x=10
Vậy có 10 dãy ghế và có 8 người trên mỗi dãy
Gọi x là số dãy ghế trong phòng họp ( x nguyên ; x>2)
Số người ngồi trên 1 dãy là \(\frac{80}{x}\)(người)
Nếu bới đi 2 dãy thì số dãy ghế còn lại là : x - 2 (dãy)
Số người ngồi trên mỗi dãy sẽ là: \(\frac{80}{x-2}\)(người )
Ta có phương trình :
\(\frac{80}{x-2}-\frac{80}{x}=2\Leftrightarrow\frac{40}{x-2}-\frac{40}{x}=1\Leftrightarrow x^2-2x-80=0\)
Giaỉ phương trình ta được \(x_1=10;x_2=-8\left(lọai\right)\)
Vậy số dãy ghế lúc đầu là 10 dãy và mỗi dãy xếp 8 người ngồi