Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hôm nay olm sẽ hướng dẫn các em giải dạng toán nâng cao sự thay đổi của phép trừ em nhé.Kiến thức cần nhớ: Khi ta tăng số bị trừ lên a đơn vị và giảm số trừ đi b đơn vị thì:
Hiệu của hai số tăng là: a + b; Hiệu mới là: hiệu cũ + a + b
Bài 1: Khi thêm vào số bị trừ 1027 đơn vị và bớt số trừ 2148 đơn vị thì được hiệu mới là:
4275 + 1027 + 2148 = 7450
Đáp số: 7450
Hiệu của hai số tăng là: a + b; Hiệu mới là: hiệu cũ + a + b
Khi thêm vào số bị trừ 1027 đơn vị và bớt số trừ 2148 đơn vị thì được hiệu mới là:
4275 + 1027 + 2148 = 7450
Đáp số: 7450

TXĐ: D = R
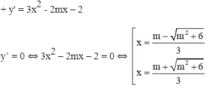
+ y’’ = 6x – 2m.
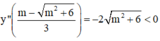
⇒ 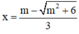 là một điểm cực đại của hàm số.
là một điểm cực đại của hàm số.
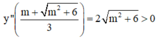
⇒ 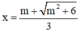 là một điểm cực tiểu của hàm số.
là một điểm cực tiểu của hàm số.
Vậy hàm số luôn có 1 điểm cực đại và 1 điểm cực tiểu.

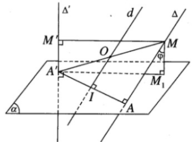
Gọi I là trung điểm của đoạn AA’. Ta có IO // Δ nên tâm O di động trên đường thẳng d cố định đi qua I và song song với ∆ . Mặt cầu tâm O đi qua hai điểm cố định A, A’ , có tâm di động trên đường trung trực d cố định của đoạn AA’. Vậy mặt cầu tâm O luôn luôn chứa đường tròn cố định tâm I có đường kính AA’ nằm trong mặt phẳng AA’ và vuông góc với d.

Nhận thấy: 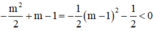 với mọi m.
với mọi m.
Suy ra, giá trị cực tiểu luôn nhỏ hơn 0 với mọi m.
Dựa vào bảng biến thiên suy ra đường thẳng y = 0 (trục hoành) luôn cắt đồ thị hàm số tại 2 điểm phân biệt (đpcm).

a) y = x 3 − (m + 4) x 2 − 4x + m
⇔ ( x 2 − 1)m + y − x 3 + 4 x 2 + 4x = 0
Đồ thị của hàm số (1) luôn luôn đi qua điểm A(x; y) với mọi m khi (x; y) là nghiệm của hệ phương trình:
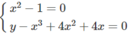
Giải hệ, ta được hai nghiệm:
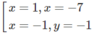
Vậy đồ thị của hàm số luôn luôn đi qua hai điểm (1; -7) và (-1; -1).
b) y′ = 3 x 2 − 2(m + 4)x – 4
Δ′ = ( m + 4 ) 2 + 12
Vì Δ’ > 0 với mọi m nên y’ = 0 luôn luôn có hai nghiệm phân biệt (và đổi dấu khi qua hai nghiệm đó). Từ đó suy ra đồ thị của (1) luôn luôn có cực trị.
c) Học sinh tự giải.
d) Với m = 0 ta có: y = x 3 – 4 x 2 – 4x.
Đường thẳng y = kx sẽ cắt (C) tại ba điểm phân biệt nếu phương trình sau có ba nghiệm phân biệt: x 3 – 4 x 2 – 4x = kx.
Hay phương trình x 2 – 4x – (4 + k) = 0 có hai nghiệm phân biệt khác 0, tức là:
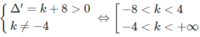




GIả sử giải đấu có \(n\)đấu thủ.
Giả sử không có bất kì hai đấu thủ nào có số trận thi đấu bằng nhau, mà số trận đã thi đấu tối đa của \(1\)đấu thủ là \(n-1\)trận (do thi đấu vòng tròn một lượt) nên số trận đã thi đấu của các đấu thủ là: \(0,1,2,...,n-1\)(trận).
Khi đó có đấu thủ chưa đấu trận nào, có đấu thủ đã đấu với \(n-1\)người còn lại (mâu thuẫn).
Do đó tại mọi thời điểm của giải, luôn có hai đấu thr có số ván đã thi đấu bằng nhau.
Cho em hỏi, có cách chứng minh nào khác không ạ. Em thấy cách chứng minh này hơi vô lý ạ