Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: B
- Nhiệt lượng toả ra của m1 kg nước để hạ nhiệt độ tới 0 0 C là :
![]()
- Nhiệt lượng cần cung cấp để 1kg nước đá tăng nhiệt độ tới 0 0 C là:
![]()
- So sánh Q t h u và Q t ỏ a ta thấy Q 1 > Q 2 . Vậy nước đá bị nóng chảy.
- Nhiệt lượng cần để nước đá nóng chảy hoàn toàn là :
![]()
- So sánh ta thấy Q 1 < Q 2 + Q 3 . Vậy nước đá chưa nóng chảy hoàn toàn.
Vậy nhiệt độ cân bằng là t = 0 0 C .

nhiệt lượng cần thiết để tăng nước đá từ - 30 đến 0 là \(Q_1=1.2100.30=63000\left(J\right)\)
nhiệt lượng cần thiết để làm tan 1 kg đá là \(Q_2=1.34.10^4=340000\left(J\right)\)
Nhiệt lượng tỏa ra khi nước hạ từ 48 đến 0 là \(Q_3=2.4200.48=403200\left(J\right)\)
Vì \(Q_3>Q_2+Q_1\) nên đá tan hết, nhiệt đọ cân bằng lớn hơn 0
Nhiệt độ cân bằng của hỗn hợp là \(\text{⇔ m1c1 ( t1 − t ) = Q1 + Q2 + m2c1 ( t − t0 ) }\)
\(\text{⇔ 2.4200. ( 48 − t ) = 63000 + 340000 + 1.4200 ( t − 0 )}\)
\(\text{⇔ 8400 ( 48 − t ) = 403000 + 4200 t }\)
\(\text{⇔ 403200 − 8400 t = 403000 + 4200 t }\)
\(\text{⇔ 200 = 12600 t ⇒ t = 0 , 016^0C }\)

Khi được làm lạnh tới 00C, nước toả ra một nhiệt lượng bằng: Q1 = m1.C1(t – 0) = 0,5.4200.20 = 42 000JĐể làm “nóng” nước đá tới 00C cần tốn một nhiệt lượng:Q2 = m2.C2(0 – t2) = 0,5.2100.15 = 15 750JBây giờ muốn làm cho toàn bộ nước đá ở 00C tan thành nước cũng ở 00C cần một nhiệt lượng là: Q3 = λ.m2 = 3,4.105.0,5 = 170 000JNhận xét:+ Q1 > Q2 : Nước đá có thể nóng tới 00C bằng cách nhận nhiệt lượng do nước toả ra+ Q1 – Q2 < Q3 : Nước đá không thể tan hoàn toàn mà chỉ tan một phần.Vậy sau khi cân bằng nhiệt được thiết lập nước đá không tan hoàn toàn và nhiệt độ của hỗn hợp là 00C

Tóm tắt:
m1 = 2kg
c1= 4200J/kg.K
t1 =48oC
m2 = 1kg
c2= 1800J/kg.K
t2 =-30oC
t=?
Giải:
Nhiệt độ cân bằng của hỗn hợp là:
Q1=Q2 (phương trình cân bằng nhiệt)
m1.c1.△t1=m2.c2.△t2
m1.c1.(t1-t)=m2.c2.(t-t2)
m1.c1.t1 - m1.c1.t = m2.c2.t - m2.c2.t2
m1.c1.t1 + m2.c2.t2 = m2.c2.t + m1.c1.t
m1.c1.t1 + m2.c2.t2 = t(m2.c2 + m1.c1)
t = \(\dfrac{m_1.c_1.t_1+m_2.c_2.t_2}{m_1.c_1+m_2.c_2}\)
t=\(\dfrac{2.4200.48+1.1800.\left(-30\right)}{2.4200+1.1800}\)\(\approx\)34,24oC
Đáp số : t \(\approx\)34,24oC

Đáp án: C
- Giả sử nhiệt độ của hỗn hợp sau khi cân bằng là 0 0 C
- Nhiệt lượng do nước tỏa ra khi hạ xuống 0 0 C là:
![]()
- Nhiệt lượng thu vào của viên nước đá để tăng nhiệt độ lên 0 0 C và tan hết tại 0 0 C là:
![]()
- Ta thấy Q t h u < Q t ỏ a chứng tỏ nước đá bị tan ra hoàn toàn.
- Gọi nhiệt độ hỗn hợp sau khi cân bằng là t 0 C (t > 0)
- Nhiệt lượng do nước tỏa ra khi hạ xuống 0 0 C là:
![]()
- Nhiệt lượng thu vào của viên nước đá để tăng nhiệt độ lên 0 0 C , tan hết tại 0 0 C và tăng lên đến t 0 C là:
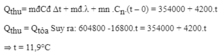

Đáp án: B
- Nhiệt lượng do xô và nước toả ra để hạ nhiệt độ xuống 0°C là:
![]()
- Nhiệt lượng thu vào của 1 viên nước đá để tăng nhiệt độ lên 0°C và tan hết tại 0°C là:
![]()
- Số viên nước đá cần phải thả vào nước là:
705000 : 83760 = 8,4
- Vậy phải thả vào xô ít nhất 9 viên đá để nhiệt độ cuối cùng trong xô là 0 0 C
giúp mình giải câu b với ạ help me