Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bước sóng \(\lambda = v/f = 1/25 = 0.04m = 4cm.\)
Độ lệch pha giữa hai nguồn sóng là \(\triangle\varphi= \varphi_2-\varphi_1 = \frac{5\pi}{6}+\frac{\pi}{6} = \pi.\)
Biên độ sóng tại điểm M là \( A_M = |2a\cos\pi(\frac{10-50}{4}-\frac{\pi}{2\pi})| =0.\)

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

Chọn đáp án C
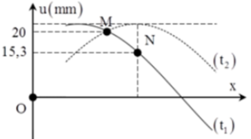
Từ hình vẽ ta xác định được: + t 1 u M = 20 m m ↑ u N = 15 , 4 m m ↑ ; t 2 u M = 20 m m ↓ u N = + A
Ta có:
cos α 2 = 20 A cos α = 15 , 3 A ⇒ 2 cos 2 α 2 − 1 = 15 , 3 A ⇔ 2 20 A 2 − 1 = 15 , 3 A ⇒ A = 21 , 6 m m
⇒ ω = 5 π r a d / s ⇒ v max = ω A = 340 m m / s

+ Từ hình vẽ ta xác định được: + t 1 u M = 20 m m ↑ u N = 15 , 4 m m ↑ ; t 2 u M = 20 m m ↓ u N = + A
+ Ta có: cos α 2 = 20 A cos α = 15 , 3 A ⇒ 2 cos 2 α 2 − 1 = 15 , 3 A ⇔ 2 20 A 2 − 1 = 15 , 3 A ⇒ A = 21 , 6 m m
⇒ ω = 5 π r a d / s ⇒ v max = ω A = 340 m m / s
Chọn đáp án C

Gọi phương trình dao động là: \(x=A\cos\omega t\)
PT vận tốc là: \(v=x'=-\omega A\sin\omega t\)
Ta có: \(A\cos\omega t_0=2\)
Cần tìm:
\(v=-\omega A\sin\omega (t_0+0,5)\)
\(=-\omega A\sin(\omega .t_0+\dfrac{2\pi}{2}.0,5)\)
\(=-\omega A\sin(\omega .t_0+\dfrac{\pi}{2})\)
\(=-\dfrac{2\pi}{2} A\cos\omega t_0\)
\(=-\dfrac{2\pi}{2}.2=-2\pi(cm/s)\)
Chọn D
 chọn A
chọn A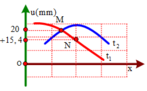
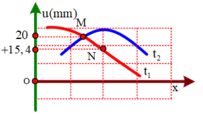
Đáp án A
Từ hình vẽ, ta xác định được
Ta có: cos α 2 = 20 A cosα = 15 , 3 A ⇒ 2 Acos 2 ( α 2 ) - 1 = 15 , 3 A
⇔ 2 ( 20 A ) 2 - 1 = 15 , 3 A ⇒ A = 21 , 6 mm .
→ Từ đây ta tìm được ω = 5 π rad / s .
→ Tốc độ cực đại v max = ωA ≈ 340 mm / s .