Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

S2quạt =2 n . pi .62/ 360 ; với n =30 độ ( sin n =3/6 =1/2 )
= 6\(\pi\) m2
Stam giác = 1/2 . 3 . \(\sqrt{6^2-3^2}\) = \(\frac{9\sqrt{3}}{2}\)
S cỏ còn lại = S hình tròn - ( S2 quạt + S tam gics ) = .............

Vận tốc trên quãng đầu là v1=700720=3536(m/s)=72(km/h)v1=700720=3536(m/s)=72(km/h)
Thế thì t/g đi AB với v/t trên là 2AB72AB7
T/g đi AB với v/t lúc sau là AB5AB5
Ta có PT: 2AB7=AB5+342AB7=AB5+34 (40'+5'=45'=3/4h)
⇔⇔ AB=8,75 (km) hay 8750 m

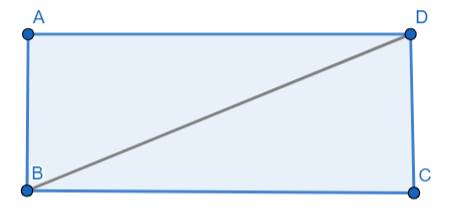
Ta có: \(AD=3AB\)
Xét tam giác vuông ABD ta có:
\(AD^2+AB^2=BD^2\)
\(\Rightarrow60^2=\left(3AB\right)^2+AB^2\)
\(\Rightarrow3600=9AB^2+AB^2\)
\(\Rightarrow3600=10AB^2\)
\(\Rightarrow AB^2=360\)
\(\Rightarrow AB=6\sqrt{10}\left(m\right)\)
\(\Rightarrow AD=3\cdot6\sqrt{10}=18\sqrt{10}\left(m\right)\)
Diện tích sân bóng là:
\(AB\cdot AD=6\sqrt{10}\cdot18\sqrt{10}=1080\left(m^2\right)\)

có trong toán vui mỗi tuần đó
Trong ba bố con, em bé là người đi chậm nhất. Ta sẽ xem cứ sau bao nhiêu phút bố và anh sẽ gặp lại em.
Bố mỗi phút đi được 40 m, em bé mỗi phút đi được 15 m. Vậy mỗi phút bố đi hơn em bé là: 40 - 15 = 25 m.
Để bố gặp lại em, thì bố phải đi hơn em bé đúng 1 vòng sân (tức là 300 mét). Suy ra bố gặp lại em bé sau: 300 : 25 = 12 phút.
Tương tự, anh lớn sẽ gặp lại em bé sau số phút là: 300 : (30 - 15) = 20 phút.
Như vậy cứ sau 12 phút thì bố sẽ gặp lại em bé; và cứ sau 20 phút anh lớn gặp lại em bé.
Bố gặp lại em bé vào các thời điểm: 12 phút, 24 phút, 36 phút, 48 phút, 60 phút, ....
Anh lớn gặp lại em bé vào các thời điểm: 20 phút, 40 phút, 60 phút, ....
Vậy cả bố và anh lớn sẽ cùng gặp lại em bé sau 60 phút [nếu các bạn đã học lớp 6 thì 60 là BCNN(12,20)].
Khi đó, bố đi được: 40 x 60 = 2400 mét; Anh lớn đi được: 30 x 60 = 1800 mét; Em bé đi được: 15 x 60 = 900 mét.

Trong ba bố con, em bé là người đi chậm nhất. Ta sẽ xem cứ sau bao nhiêu phút bố và anh sẽ gặp lại em.
Bố mỗi phút đi được 40 m, em bé mỗi phút đi được 15 m. Vậy mỗi phút bố đi hơn em bé là: 40 - 15 = 25 m.
Để bố gặp lại em, thì bố phải đi hơn em bé đúng 1 vòng sân (tức là 300 mét). Suy ra bố gặp lại em bé sau: 300 : 25 = 12 phút.
Tương tự, anh lớn sẽ gặp lại em bé sau số phút là: 300 : (30 - 15) = 20 phút.
Như vậy cứ sau 12 phút thì bố sẽ gặp lại em bé; và cứ sau 20 phút anh lớn gặp lại em bé.
Bố gặp lại em bé vào các thời điểm: 12 phút, 24 phút, 36 phút, 48 phút, 60 phút, ....
Anh lớn gặp lại em bé vào các thời điểm: 20 phút, 40 phút, 60 phút, ....
Vậy cả bố và anh lớn sẽ cùng gặp lại em bé sau 60 phút [nếu các bạn đã học lớp 6 thì 60 là BCNN(12,20)].
Khi đó, bố đi được: 40 x 60 = 2400 mét; Anh lớn đi được: 30 x 60 = 1800 mét; Em bé đi được: 15 x 60 = 900 mét.
Trong ba bố con, em bé là người đi chậm nhất. Ta sẽ xem cứ sau bao nhiêu phút bố và anh sẽ gặp lại em.
Bố mỗi phút đi được 40 m, em bé mỗi phút đi được 15 m. Vậy mỗi phút bố đi hơn em bé là: 40 - 15 = 25 m.
Để bố gặp lại em, thì bố phải đi hơn em bé đúng 1 vòng sân (tức là 300 mét). Suy ra bố gặp lại em bé sau: 300 : 25 = 12 phút.
Tương tự, anh lớn sẽ gặp lại em bé sau số phút là: 300 : (30 - 15) = 20 phút.
Như vậy cứ sau 12 phút thì bố sẽ gặp lại em bé; và cứ sau 20 phút anh lớn gặp lại em bé.
Bố gặp lại em bé vào các thời điểm: 12 phút, 24 phút, 36 phút, 48 phút, 60 phút, ....
Anh lớn gặp lại em bé vào các thời điểm: 20 phút, 40 phút, 60 phút, ....
Vậy cả bố và anh lớn sẽ cùng gặp lại em bé sau 60 phút [nếu các bạn đã học lớp 6 thì 60 là BCNN(12,20)].
Khi đó, bố đi được: 40 x 60 = 2400 mét; Anh lớn đi được: 30 x 60 = 1800 mét; Em bé đi được: 15 x 60 = 900 mét.

Gọi chiều rộng là x
=>Chiều dài là x+10
Theo đề, ta có: x^2+(x+10)^2=50^2
=>2x^2+20x-2400=0
=>x^2+10x-1200=0
=>(x+40)(x-30)=0
=>x=30
Diện tích là 30*40=1200m2

gọi chiều rộng = a => chiều dài = a+10
Áp dụng định lý Pytago => a^2 + (a+10)^2 = độ dài đường chéo ^2 = 1300
=> 2a^2 +20a +100=1300
=> a^2 +10a-600 = 0
=> (a+30)(a-20) =0
=> a=20
=> chu vi sân bóng = 2(a+a+10) = 2.50 =100