Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

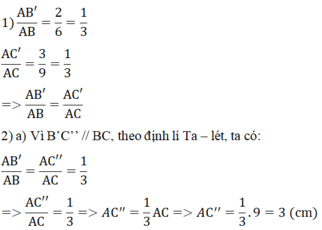
b) Trên đoạn thẳng AC ta có: AC’= AC’’= 3 cm nên
Khi đó, hai đường thẳng BC và B’C’ song song với nhau.

Lời giải :
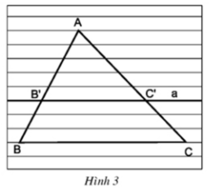
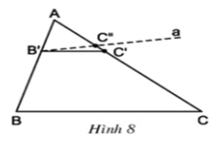
A B C B' C' a C''
Ta có : \(\frac{AB'}{AB}=\frac{AC'}{AC}\)( GT ) ( 1 )
+) Đường thẳng a đi qua B' song song với BC ( GT )
\(B'C''//BC\)( vì đường thẳng a cắt AC tại C'' )
\(\Rightarrow\frac{AB'}{AB}=\frac{AC''}{AC}\)( Định lí Ta lét ) ( 2 )
Từ ( 1 ) và ( 2 )
\(\Rightarrow AC'=AC''\)

a) Ta có:
\(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3}\) và \(\frac{{AC'}}{{AC}} = \frac{5}{{15}} = \frac{1}{3}\).
b) Vì \(B'E//BC\) và\(B'E\) cắt \(AC\) tại \(E\) nên theo định lí Thales ta có:
\(\frac{{AB'}}{{AB}} = \frac{{AE}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AE}}{{15}} \Rightarrow AE = \frac{{2.15}}{6} = 5cm\)
c) Ta có: \(AE = AC' = 5cm\).
d) Điểm \(E \equiv C'\) và đường thẳng \(B'C' \equiv B'E\).

A B D C F E
Vì DF//AB (gt) . Áp dụng định lý Talet ta có : \(\frac{AF}{AC}=\frac{BD}{BC}\)(1)
Vì DE//AC (gt) . Áp dụng định lý Talet ta có : \(\frac{AE}{AB}=\frac{CD}{BC}\)(2)
Từ (1);(2) \(\Rightarrow\frac{AE}{AB}+\frac{AF}{AC}=\frac{BD}{BC}+\frac{CD}{BC}=\frac{BD+CD}{BC}=\frac{BC}{BC}=1\)(Đpcm)
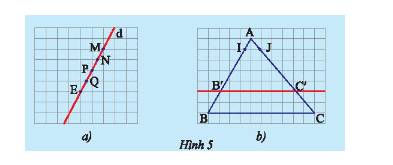
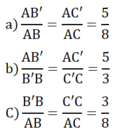
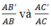
a) Độ dài các đoạn thẳng \(MN;NP;PQ\) và \(QE\) đều bằng nhau vì chúng đều bằng độ dài đường chéo của một hình vuông nhỏ.
b) Trên cạnh \(AB\), lấy đoạn \(AI\) làm đơn vị đo nên độ dài \(AB' = 5AI;BB' = 2AI;\) Trên \(AB = 7AI\); cạnh \(AC\), lấy đoạn \(AJ\) làm đơn vị đo nên độ dài \(AC' = 5AJ;C'C = 2AJ\);\(AC = 7AJ\).
Tỉ số \(AB'\) và \(B'B\) là \(AB':B'B = \frac{{AB'}}{{B'B}} = \frac{{5AI}}{{2AI}} = \frac{5}{2}\);
Tỉ số \(AC'\) và \(C'C\) là \(AC':C'C = \frac{{AC'}}{{C'C}} = \frac{{5AJ}}{{2AJ}} = \frac{5}{2}\).
Do đó, \(\frac{{AB'}}{{B'B}} = \frac{{AC'}}{{C'C}} = \frac{5}{2}\).
Ta có: \(\frac{{AB'}}{{AB}} = \frac{{5AI}}{{7AI}} = \frac{5}{7};\frac{{AC'}}{{AC}} = \frac{{5AJ}}{{7AJ}} = \frac{5}{7}\).
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{5}{7}\).
Ta có: \(\frac{{B'B}}{{AB}} = \frac{{2AI}}{{7AI}} = \frac{2}{7};\frac{{C'C}}{{AC}} = \frac{{2AJ}}{{7AJ}} = \frac{2}{7}\).
Do đó, \(\frac{{AB'}}{{AB}} = \frac{{AC'}}{{AC}} = \frac{2}{7}\).