Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
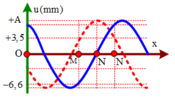
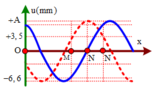
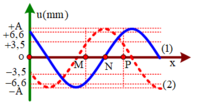
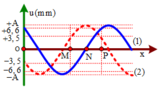
Từ đồ thị ta thấy rằng hai thời điểm t 1 v à t 2 vuông pha nhau, do vậy
Δ t = 0 , 5 = 2 k + 1 T 4 ⇒ ω = 2 k + 1 π r a d / s
Tại thời điểm t 1 điểm N đang đi qua vị trí cân bằng theo chiều âm do vậy tốc độ của N sẽ là: v N 1 = v max = ω A = 7 , 5 π 2 k + 1 m m / s
Vận tốc của N tại thời điểm t 0 = t 1 − 1 9 s : v N 0 = − v N 1 cos 2 k + 1 π 9 m m / s (mm/s)
Với k = 1, ta thu được vN = -3,53 cm/s

+ Ta để ý rằng điểm N tại thời điểm t1 đang ở VTCB, tại thời điểm t2, N đi đến vị trí bên → t1 và t2 là hai thời điểm vuông pha thỏa mãn
+ Δ t = 0 , 5 = 2 k + 1 T 4 u 1 N A 2 + u 2 N A 2 = 1 ⇒ T = 2 2 k + 1 A = 2 11 2 + 3 , 5 2 = 7 , 5 m m
+ Với k = 0 ⇒ T = 2 s ω = π r a d . s − 1
+ Tốc độ của vật tại thời điểm t 0 = t 1 − 1 9 s : v N = − ω A cos ω 1 9 ≈ 21 m m / s
+ Với k = 1 ⇒ T = 2 3 s ω = 3 π r a d . s − 1
+ Tốc độ của vật tại thời điểm t 0 = t 1 − 1 9 s : v N = − ω A cos ω 1 9 ≈ 21 m m / s
Chọn đáp án D

Chọn đáp án D
@ Lời giải:
+ Ta để ý rằng điểm N tại thời điểm t 1 đang ở VTCB, tại thời điểm t 2 , N đi đến vị trí bên → t 1 và t 2 là hai thời điểm vuông pha thỏa mãn
+
Δ
t
=
0
,
5
=
2
k
+
1
T
4
u
1
N
A
2
+
u
2
N
A
2
=
1
⇒
T
=
2
2
k
+
1
A
=
2
11
2
+
3
,
5
2
=
7
,
5
m
m
+ Tốc độ của vật tại thời điểm
t
0
=
t
1
−
1
9
s
:
v
N
=
−
ω
A
cos
ω
1
9
≈
21
m
m
/
s
+ Với k = 0 ⇒ T = 2 s ω = π r a d . s − 1
+ Với k = 1 ⇒ T = 2 3 s ω = 3 π r a d . s − 1
+ Tốc độ của vật tại thời điểm t 0 = t 1 − 1 9 s : v N = − ω A cos ω 1 9 ≈ − 3 , 53 c m / s

Áp dụng công thức: \(A^2 = x^2 +\frac{v^2}{\omega^2} \) \(\Rightarrow A^2 = 3^2 +\frac{(60\sqrt3)^2}{\omega^2} = (3\sqrt2)^2 +\frac{(60\sqrt2)^2}{\omega^2} \)
Giải hệ trên ta được \(\omega = 20rad/s; \ A =6cm\)

\(\omega_1=\frac{2\pi}{T_1}=\frac{10\pi}{3}\); \(\omega_2=\frac{2\pi}{T_2}=\frac{10\pi}{9}\)
\(\varphi_2=\omega_2t;\omega_1t=\pi-\varphi_2\)
\(\Rightarrow t=\frac{\pi}{\omega_1+\omega_2}=0,225\left(s\right)\)

Bước sóng \(\lambda = v/f = 1/25 = 0.04m = 4cm.\)
Độ lệch pha giữa hai nguồn sóng là \(\triangle\varphi= \varphi_2-\varphi_1 = \frac{5\pi}{6}+\frac{\pi}{6} = \pi.\)
Biên độ sóng tại điểm M là \( A_M = |2a\cos\pi(\frac{10-50}{4}-\frac{\pi}{2\pi})| =0.\)
 chọn A
chọn A
+ Từ đồ thị ta thấy rằng hai thời điểm t1 và t2 vuông pha nhau, do vậy
Δ t = 0 , 5 = 2 k + 1 T 4 ⇒ ω = 2 k + 1 π r a d / s
+ Tại thời điểm t1 điểm N đang đi qua vị trí cân bằng theo chiều âm do vậy tốc độ của N sẽ là:
v N 1 = v max = ω A = 7 , 5 π 2 k + 1 m m / s
+ Vận tốc của N tại thời điểm t 0 = t 1 − 1 9 s : v N 0 = − v N 1 cos 2 k + 1 π 9 m m / s (mm/s)
Với k = 1, ta thu được vN = -3,53 cm/s
Chọn đáp án B