Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

chọn hệ quy chiếu: gốc tọa độ trùng A
chiều dượng của Ox từ A đến B
gốc thời gian khi ô tô đi qua điểm A ( lúc 8h)
a) phương trình chuyển động của 2 xe
x1=10t - 0,1t^2
x2= 560 - 0,2t^2
2 xe gặp nhau <=> x1=x2
<=> t=40s
x=x1=x2= 240m
b) phương trình vận tốc của 2 xe: (v=v0 + at)
v1=10 - 0,2 .40 =2 m/s
v2= 0+ 0,4 .40 = 16 m/s
Chọn gốc thời gian là lúc 8h, gốc tọa độ tại A, chiều dương từ A đến B
ô tô 1: xo1 = 0; vo1 = 10m/s; a1 = -0,2m/s2
ô tô 2: xo1 = 560; vo1 = 0; a1 = 0,4m/s2
Giải
a) Phương trình chuyển động của hai xe:
x1 = x01 + v01t + 0,5a1t2 = 10t – 0,1t2 (1)
x2 = x02 + v02t + 0,5a2t2 = 560 – 0,2t2 (2)
b) Khi hai xe gặp nhau:
x1 = x2 => 10t – 0,1t2 = 560 – 0,2t2 => t = 40 s
=> x1 = x2 = 240 m.
c) Thời gian để xe một dừng lại:
v1 = vo1 + a1.t => t = 50 s;

a)-Chọn hệ quy chiếu có chiều (+) trục Õ là từ A\(\Rightarrow\)B
-Chọn gốc toạ độ (O) tại A
-Chọn gốc thời gian (to=O)
+Xe thứ nhất có:\(\left\{{}\begin{matrix}v_{o1}=4m/s\\a_{o1}=0,2m/s^2\\x_1=0m\end{matrix}\right.\)
+Xe thứ hai có:\(\left\{{}\begin{matrix}V_{o1}=1m/s\\a_1=0,2m/s^2\\x_1=200m\end{matrix}\right.\)
-PTCĐ của xe thứ nhất và xe thứ hai lần lược là :
x=xo+vot+\(\dfrac{1}{2}\)at2
\(\Rightarrow\)x1=4t+\(\dfrac{1}{2}\).0,2t2
\(\Rightarrow\)x2=200+1.t+\(\dfrac{1}{2}\).0,1.t2
b)khi hai xe gặp nhau thì toạ đọ hai xe bằng nhau nên:
x1=x2
\(\Rightarrow\)4t+\(\dfrac{1}{2}\).0,2t2=200+1.t+\(\dfrac{1}{2}\).0,1.t2
\(\Rightarrow\)0,05t2+3t−200=0
\(\Rightarrow\)\(\left\{{}\begin{matrix}t_1=40\\t_2=-100\end{matrix}\right.\)(t1 nhận; t2 loại)
Vị trí của hai xe lúc gặp nhau là:x1=x2=200+1.40+\(\dfrac{1}{2}\).0,1.402=320(m)
vậy vị trí của hai xe lúc gặp nhau là 320m và thời gian hai xe gặp nhau là 40m/s2

Chọn trục tọa độ nằm trên đường thẳng AB, chiều dương hướng từ A đến B, gốc tọa độ là A.
(xA = 0, xB = 125)
Vật thứ nhất,đi từ A đến B, có gia tốc +2 m/s², vận tốc đầu +4 m/s, tọa độ đầu 0,
có phương trình chuyển động là: x₁(t) = 1t² + 4t + 0, (t > 0
Vật thứ nhì , đi từ B đến A, có gia tốc −4 m/s², vận tốc đầu −6 m/s, tọa độ đầu +125,
có phương trình chuyển động là: x₂(t) = −2t² − 6t + 125, (t > 0)
(1a)
Thời điểm hai vật gặp nhau là thời điểm t > 0 sao cho
x₁(t) = x₂(t)
1t² + 4t = −2t² − 6t + 125, (t > 0)
3t² + 10t − 125 = 0, (t > 0)
Giải phương trình ta được t = 5 s
Vị trí lúc hai vật gặp nhau là
x₁(5) = 5² + 4×5 = 45 m
(1b)
Giả sử hai vật không va chạm khi gặp nhau và tiếp tục di chuyển với gia tốc không đổi đã cho.
Gọi v₀ là vận tốc đầu, v là vận tốc cuối sau khi đi hết quãng đường AB hay BA
Ta có công thức v² = v₀² + 2as
Đối với vật thứ nhất:
v₀ = +4 m/s, a = +2 m/s², s = (xB − xA) = 135 m,
Do đó:
v₁² = 4² + 2×2×125 = 516 (m/s)²,
Vì vật thứ nhất đi theo chiều dương nên v₁ > 0
v₁ = +√516 ≈ +22,72 m/s
Đối với vật thứ nhì:
v₀ = −6 m/s, a = −4 m/s², s = (xA − xB) = −135 m,
Do đó:
v₂² = 6² + 2×(-4)×(-125) = 1036 (m/s)²,
Vì vật thứ nhì đi theo chiều âm nên v₂ < 0
v₂ = −√1036 ≈ −32,19 m/s

Gọi \(t\left(s\right)\)là thời gian để hai xe đuổi kịp nhau. \(\left(t>0\right)\)
Ta có: \(4t+\frac{1}{2}.0,2t^2=200+1.t+\frac{1}{2}.0,1.t^2\)
\(\Leftrightarrow\frac{1}{20}t^2+3t-200=0\)
\(\Leftrightarrow\orbr{\begin{cases}t=40\left(tm\right)\\t=-100\left(l\right)\end{cases}}\)
Vị trí hai xe gặp nhau cách A quãng đường là: \(4.40+\frac{1}{2}.0,2.40^2=320\left(m\right)\)

Giải:
Chọn chiều dương là chiều từ đỉnh đến chân dốc, gốc toạ độ tại đỉnh A, gốc thời gian là lúc xe A xuống dốc.
Đối với xe A:
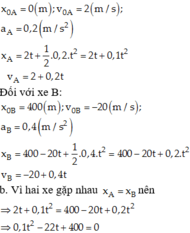

Thay thời gian loại nghiệm ta có hai thời điểm vật cách nhau 40m là

Chọn chiều dương là chiều từ đỉnh đến chân dốc, gốc toạ độ tại đỉnh A, gốc thời gian là lúc xe A xuống dốc.
Đối với xe A:
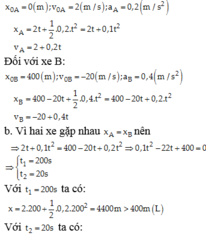
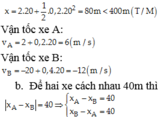
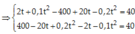
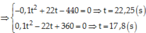
Thay thời gian loại nghiệm ta có hai thời điểm vật cách nhau 40m là

a,ta có gốc A chiều + AB => X1=Xo+Vot+1/2at^2 vs Xo=0; Vo=10 ;a=-0.2(chậm dần)
=>X1=10t-0.1t^2
xe2 ở B có Xo=560 ,Vo=0 ,a=0.4 => X2=560-0.2t^2 ( xe 2 đi ngược lại B>A )
b,2 xe gặp nhau khi X1=X2 <=> 10t-0.1t^2=560-0.2t^2 <=> t=40(n) t=-140(l)
S1=Vot+1/2at^2=10*40 -0.1*40^2=240
S2=Vot+1/2at^2=0.2*40^2=320
c,tại thời điểm 2 xe gặp nhau t=40 => v xe1 lúc gặp nhau ;V1=Vo-at=10-0.2*40=2
V2=Vo +at=0.4*40=16
vẽ trục oy là v; ox là t trên oy lấy các điểm 2,10,16 trên ox lấy điểm 40 . vẽ đt x1 từ 10 đến giao điểm của 2 vs 40 . vẽ x2 từ 0 đến giao 16 vs 40

A O x
1) Chọn trục tọa độ Ox như hình vẽ, mốc thời gian lúc ô tô xuất phát.
- Phương trình vận tốc: \(v=v_0+a.t\)
Ban đầu, \(v_0=0\); \(a=0,5m/s^2\)
Suy ra: \(v_1=0,5.t(m/s)\)
- Phương trình tọa độ: \(x=x_0+v_0.t+\dfrac{1}{2}a.t^2\)
\(x_0=0\); \(v_0=0\); \(a=0,5(m/s^2)\)
Suy ra: \(x_1=\dfrac{1}{2}.0,5.t^2=0,25.t^2(m)\)
2) Đổi \(v_{02}=18km/h=5m/s\)
a) Phương trình chuyển động của tàu điện là:
\(x_2=x_0+v_0.t+\dfrac{1}{2}a.t^2=0+5.t+\dfrac{1}{2}.0,3.t^2\)
\(\Rightarrow x_2=5.t+0,15.t^2(m)\)
Ô tôt đuổi kịp tàu điện khi: \(x_1=x_2\)
\(\Rightarrow 0,25.t^2=5.t+0,15.t^2\)
\(\Rightarrow t = 50(s)\)
Vị trí gặp nhau là: \(x=0,25.50^2=625(m)\)
b) Thay \(t=50s\) vào phương trình vận tốc của ô tô và tàu điện ta được:
Vận tốc của ô tô: \(v_1=0,5.t=0,5.50=25(m/s)\)
Vận tốc của tàu điện: \(v_2=5+0,3.t=5+0,3.50=20(m/s)\)
Bạn ơi " cđtndđ " và " cđtcdđ " là gì thế ?
Chuyển động nhanh dần đều và chuyển động chậm dần đều đó