Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A 2 y -2 -2 4 B C x
Vì G là trọng tâm tam giác ABC, nên ta có :
\(\overrightarrow{MA}=3\overrightarrow{MG}\Leftrightarrow\left(x_A-1;y_A+1\right)=3\left(\frac{2}{3}-1;0+1\right)\Leftrightarrow\begin{cases}x_A-1=1\\y_A+1=3\end{cases}\)
\(\Leftrightarrow A\left(0;2\right)\)
Giả sử \(B\left(x_1;y_1\right);C\left(x_2;y_2\right)\)
Vì M là trung điểm của BC, nên ta có :
\(\begin{cases}x_1+x_2=2\\y_1+y_2=-2\end{cases}\)\(\Leftrightarrow\begin{cases}x_2=2-x_1\\y_2=-2-y_1\end{cases}\)
Vậy \(C\left(2-x_1;-2-y_1\right)\)
Ta có \(\overrightarrow{BA}=\left(-x_1;2-y_1\right);\overrightarrow{CA}=\left(x_1-2;y_1+4\right)\)
Vì \(\widehat{BAC}=90^0\) nên \(\overrightarrow{BA}.\overrightarrow{CA}=0\)
\(\Leftrightarrow-x_1\left(x_1-2\right)+9y_1+4\left(2-y_1\right)=0\)
\(\Leftrightarrow-x^2_1-y^2_1+2x_1-2y_1+8=0\) (1)
Do AB = AC nên \(AB^2=AC^2\)
\(x^2_1+\left(y_1-2\right)^2=2\left(2-x_1\right)^2+\left(4-y_1\right)^2\)
\(\Leftrightarrow-4y_1+4=-4x_1+4+16+8y_1\)
\(\Leftrightarrow x_1=3y_1+4\) (2)
Thay (2) vào (1) ta có :
\(y^2_1+y_1=0\Leftrightarrow\begin{cases}y_1=0\\y_1=-2\end{cases}\)
Từ đó ta có :
\(B\left(4;0\right);C\left(-2;-2\right)\) hoặc \(B\left(-2;-2\right);C\left(4;0\right)\)
Tóm lại ta có :
\(A\left(0;2\right);B\left(4;0\right);C\left(2;-2\right)\) là 3 đỉnh của tam giác cần tìm
(Tam giác kia vẫn là tam giác trên chỉ đổi B và C với nhau)
Vì G là trọng tâm của tam giác ABC nên ta có :
\(\overrightarrow{MA}=3\overrightarrow{MG}\Leftrightarrow\left(x_A-1;y_A+1\right)=3\left(\frac{2}{3}-1;0+1\right)\Leftrightarrow\begin{cases}x_A-1=-1\\y_A+1=3\end{cases}\)
\(\Leftrightarrow A\left(0;2\right)\)
Ta thấy MA có hệ số góc
\(k=\frac{2-\left(-1\right)}{0-1}=-3\)
Vì \(BC\perp MA\) nên đường thẳng nối BC có hệ số góc là \(\frac{1}{3}\), do đó phương trình của nó là :
\(y=\frac{1}{3}\left(x-1\right)-1\Leftrightarrow x-3y-4=0\)
Mặt khác do :
\(MB=MC=MA=\sqrt{1^2+3^2}=\sqrt{10}\)
Vậy tọa độ của B, C thỏa mãn phương trình đường tròn tâm M, bán kính =\(\sqrt{10}\)
\(\left(x-1\right)^2+\left(y+1\right)^2=10\)
Vậy tọa độ của B, C là nghiệm của hệ phương trình :
\(\begin{cases}x-3y-4=0\\\left(x-1\right)^2+\left(y+1\right)^2=10\end{cases}\)
Giải hệ phương trình ta có các nghiệm (4;0) và (-2;2)
Vậy A(0;2);B(4;0);C(-2;-2) là 3 đỉnh của tam giác cần tìm

Ta có: = (1; 7);
= (1; 7)
=
=> ABCD là hình bình hành (1)
ta lại có : AB2 = 50 => AB = 5 √2
AD2 = 50 => AD = 5 √2
AB = AD, kết hợp với (1) => ABCD là hình thoi (2)
Mặt khác = (1; 7);
= (-7; 1)
1.7 + (-7).1 = 0 => ⊥
(3)
Kết hợp (2) và (3) suy ra ABCD là hình vuông


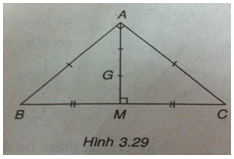

Tam giác ABC có M; N ; P lần lượt là trung điểm của BC; AC ; BC nên PM và MN là đường trung bình của tam giác ABC.
Suy ra: PM// AC; NM // AB.
Do đó, tứ giác ANMP là hình bình hành.