Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

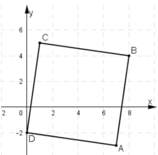
Ta có: = (1; 7);
= (1; 7)
=
=> ABCD là hình bình hành (1)
ta lại có : AB2 = 50 => AB = 5 √2
AD2 = 50 => AD = 5 √2
AB = AD, kết hợp với (1) => ABCD là hình thoi (2)
Mặt khác = (1; 7);
= (-7; 1)
1.7 + (-7).1 = 0 => ⊥
(3)
Kết hợp (2) và (3) suy ra ABCD là hình vuông

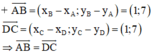
⇒ ABCD là hình bình hành.
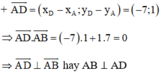
⇒ hình bình hành ABCD là hình chữ nhật.
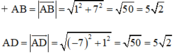
⇒ AB = AD ⇒ Hình chữ nhật ABCD là hình vuông (ĐPCM).

Giả sử \(C\left(c;-c;-3\right)\in d_1\)
\(D\left(5d+16;d\right)\in d_2\)
\(\Rightarrow\overrightarrow{CD}=\left(5d+16-c;d+c+3\right)\)
ABCD là hình bình hành \(\Rightarrow\overrightarrow{CD}=\overrightarrow{BA}=\left(3;4\right)\)
\(\Rightarrow\begin{cases}5d+16-c=3\\d+c+3=4\end{cases}\)\(\Leftrightarrow\begin{cases}5d-c=-13\\d+c=1\end{cases}\)
\(\Leftrightarrow\begin{cases}d=-2\\c=3\end{cases}\)
\(\Rightarrow C\left(3;-6\right);D\left(6;-2\right)\)
Ta có : \(\overrightarrow{BA}=\left(3;4\right);\overrightarrow{BC}=\left(4;-3\right)\) không cùng phương => A, B, C, D không thẳng hàng => ABCD là hình bình hàng
Vậy \(C\left(3;-6\right);D\left(6;-2\right)\)

Muốn chứng minh tứ giác ABCD là hình thang cân ta cần chứng minh hai điều:
- AB//CD.
- AD = BC.
\(\overrightarrow{AB}\left(1;1\right);\overrightarrow{DC}\left(-3;-3\right)\)
Dễ thấy \(\overrightarrow{DC}=-3\overrightarrow{AB}\) nên hai véc tơ \(\overrightarrow{DC}\) và \(\overrightarrow{AB}\) cùng phương.
Suy ra DC//AB. (1)
\(AD=\sqrt{\left(0-1\right)^2+\left(-2-1\right)^2}=\sqrt{10}\).
\(BC=\sqrt{\left(3-0\right)^2+\left(1-2\right)^2}=\sqrt{10}\).
Vậy AD = BC. (2)
Từ (1) và (2) suy ra tứ giác ABCD là hình thang cân.

a) D nằm trên trục Ox nên tọa độ của D là (x; 0).
Ta có :
DA2 = (1 – x)2 + 32
DB2 = (4 – x)2 + 22
DA = DB => DA2 = DB2
<=> (1 – x)2 + 9 = (4 – x)2 + 4
<=> 6x = 10
=> x = => D(
; 0)

b)
OA2 = 12 + 32 =10 => OA = √10
OB2 = 42 + 22 =20 => OA = √20
AB2 = (4 – 1)2 + (2 – 3)2 = 10 => AB = √10
Chu vi tam giác OAB: √10 + √10 + √20 = (2 + √2)√10.
c) Ta có = (1; 3)
= (3; -1)
1.3 + 3.(-1) = 0 => .
= 0 =>
⊥
SOAB = |
| .|
| => SOAB =5 (dvdt)

a)Gọi \(D\left(x;y\right)\) là tọa độ điểm cần tìm.
\(\overrightarrow{AD}\left(x-2;y-4\right)\); \(\overrightarrow{BC}\left(2;-4\right)\).
Tứ giác ABCD là hình bình hành khi và chỉ khi:
\(\overrightarrow{AD}=\overrightarrow{BC}\)\(\Leftrightarrow\left\{{}\begin{matrix}x-2=2\\y-4=-4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=0\end{matrix}\right.\)\(\Rightarrow D\left(4;0\right)\).
b) Gọi\(A'\left(x;y\right)\) là điểm cần tìm. A' thỏa mãn hai điều sau:
- \(AA'\perp BC\). (1)
- A' , B, C thẳng hàng. (2)
\(\overrightarrow{AA'}\left(x-2;y-4\right)\); \(\overrightarrow{BC}\left(2;-4\right)\).
\(\left(1\right)\Leftrightarrow\overrightarrow{AA'}.\overrightarrow{BC}=\overrightarrow{0}\)\(\Leftrightarrow2\left(x-2\right)-4\left(y-4\right)=0\) (3)
(2) suy ra hai véc tơ \(\overrightarrow{A'B}\) và \(\overrightarrow{BC}\) cùng phương.
Có \(\overrightarrow{A'B}\left(1-x;3-y\right)\).
Nên \(\dfrac{1-x}{2}=\dfrac{3-y}{4}\) (4)
Từ (3) và (4) suy ra: \(\left\{{}\begin{matrix}x=1\\y=3\end{matrix}\right.\).
Vậy A'(1;3).

Ta có: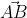 = (1; 7);
= (1; 7); 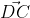 = (1; 7)
= (1; 7)
ta lại có : AB2 = 50 => AB = 5 √2
AD2 = 50 => AD = 5 √2
AB = AD, kết hợp với (1) => ABCD là hình thoi (2)
Mặt khác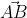 = (1; 7);
= (1; 7); 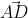 = (-7; 1)
= (-7; 1)
1.7 + (-7).1 = 0 =>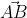 ⊥
⊥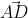 (3)
(3)
Kết hợp (2) và (3) suy ra ABCD là hình vuông
Sao AB^2 lại =50 ạ