Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Giải:
Đặt \(z=a+bi\) với $a,b$ là các số thực
Ta có:
\(|z-i|=|(1+i)z|\Leftrightarrow |a+i(b-1)|=|z||1+i|=|a+bi|\sqrt{2}\)
\(\Leftrightarrow a^2+(b-1)^2=2(a^2+b^2)\)
\(\Leftrightarrow a^2+(b+1)^2=2\)
Vậy tập hợp biểu diễn số phức $z$ nằm trên đường tròn tâm \((0,-1)\) bán kính \(R=\sqrt{2}\)
Giải:
Đặt \(z=a+bi\) với $a,b$ là các số thực
Ta có:
\(|z-3+4i|=2\Leftrightarrow |(a-3)+i(b+4)|=2\)
\(\Leftrightarrow (a-3)^2+(b+4)^2=4\)
Vậy tập hợp các điểm biểu diễn số phức $z$ nằm trên đường tròn tâm \((3;-4)\) bán kính \(R=2\)
Giả sử z = x + yi, (x,y ε R), khi đó trên mặt phẳng toạ độ Oxy, điểm M(x;y) biểu diễn số phức z.
a) Ta có |z| = 1 ⇔ 
= 1 ⇔ x2 + y2 = 1.
Vậy tập hợp điểm biểu diễn số phức z là đường tròn tam O, bán kính bằng 1
b) Ta có |z| ≤ 1 ⇔ ≤ 1 ⇔ x2 + y2 ≤ 1.
Vậy tập hợp điểm biểu diễn số phức z là hình tròn tâm O, bán kính bằng 1 (kể cả các điểm trên đường tròn) (hình b)
c) Ta có 1 < |z| ≤ 2 ⇔ 1 < ≤ 2 ⇔ 1 < x2 + y2 ≤ 4.
Vậy tập hợp điểm biểu diễn số phức z là phần nằm giữa đường tròn tâm O, bán kính bằng 1 (không kể điểm trên đường tròn này) và đường tròn tâm O, bán kính bằng 2 (kể cả các điểm trên đường tròn này)
d) Ta có |z| = 1 ⇔ = 1 ⇔ x2 + y2 = 1 và phần ảo của z bằng 1 tức y = 1. Suy ra x = 0 và y = 1
Vậy tập hợp các điểm cần tìm là điểm A(0;1)
Tập hợp các điểm biểu diễn các số phức z là các hình sau:
a) Ta có x = 1, y tùy ý nên tập hợp các điểm biểu diễn z là đường thẳng x = 1 (hình a)
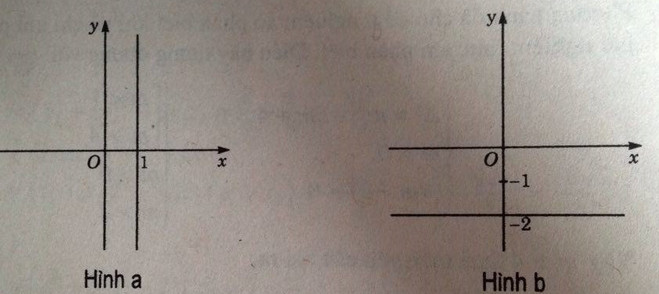
b) Ta có y = -2, x tùy ý nên tập hợp các điểm biểu diễn z là đường thẳng y = -2 (hình b)
c) Ta có x ∈ [-1, 2] và y ∈ [0, 1] nên tập hợp các điểm biểu diễn z là hình chữ nhật sọc (hình c)
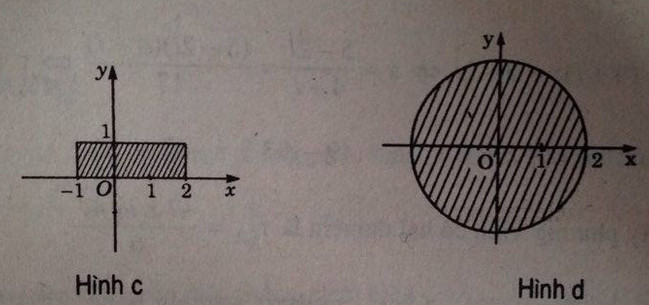
d) Ta có:
|z|≤2⇔√x2+y2≤2⇔x2+y2≤4|z|≤2⇔x2+y2≤2⇔x2+y2≤4
Vậy tập hợp các điểm biểu diễn z là hình tròn tâm O (gốc tọa độ) bán kính bằng 2 (kể cả các điểm trên đường tròn) (hình d)
\(A=\left(\frac{1+i}{1-i}\right)^{11}=\left(i\right)^{11}=i\cdot\left(i^2\right)^5=-i\)
\(B=\left(\frac{2i}{1+i}\right)^8=\left(1+i\right)^8=\left[\left(1+i\right)^2\right]^4=\left(2i\right)^4=16\)
\(\Rightarrow\overline{z}=16-i\Leftrightarrow z=16+i\)
Vậy \(\left|\overline{z}+iz\right|=\left|15+15i\right|=15\sqrt{2}\)
Dạ cảm ơn ạ
Chọn A