Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Gọi khoảng cách từ một điểm bất kỳ thuộc CD đến các nguồn A, B tương ứng là d 2 và d 1
Ta có AD − BD ≤ d 2 − d 1 ≤ AC − BC
+ Điểm cực đại trên đoạn CD thỏa mãn: d 2 − d 1 = kλ, k = 0, ± 1, ± 2, ± 3 ... với ⇒ AD − BD ≤ kλ ≤ AC − BC ⇔ AD − BD λ ≤ k ≤ AC − BC λ
⇒ − 3 , 3 ≤ k ≤ 3 , 3
Có 7 giá trị của k là 0, ± 1, ± 2, ± 3 nên có 7 điểm cực đại trên CD
+ Điểm cực tiểu trên đoạn CD thỏa mãn: d 2 − d 1 = 2 k + 1 λ 2 , với k = 0, ± 1, ± 2, ± 3 ...
⇒ AD − BD ≤ 2 k + 1 λ 2 ≤ AC − BC ⇔ 2 AD − BD λ ≤ 2k + 1 ≤ 2 AC − BC λ ⇒ − 3 , 8 ≤ k ≤ − 2 , 83
Có 6 giá trị của k thỏa mãn k = 0, ± 1, ± 2, − 3 , − 2 nên có 6 điểm cực tiểu trên CD

ü Đáp án A
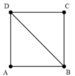
+ Số dãy cực đại giao thoa
- A B λ ≤ k ≤ A B λ ⇔ - 5 , 3 ≤ k ≤ 5 , 3
→ có 11 dãy
+ Xét tỉ số: A D - B D λ = - 2 , 2
→ Trên BD có 7 cực đại dao thoa ứng với k = –1….5

+ Điểm M ngược pha với nguồn A khi:
![]()

+ Vì C và D đối xứng qua AB nên ta sẽ tìm số điểm ngược pha trên OC, sau đó lấy đối xứng suy ra trên CD.
+ Từ hình vẽ ta có:

=> Trên OC có hai điểm
+ Do tính đối xứng nên trên CD có bốn điểm => Chọn B.

Chọn C.
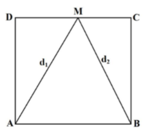
Bước sóng: λ = v/f
Độ lệch pha hai sóng kết hợp tại M:
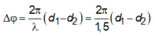
Biên độ dao động tổng hợp tại M:
![]()
![]()
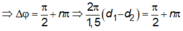
![]()
Điều kiện để M nằm trên CD là
![]()
![]()
![]()
=> n = -6,..,5 có 12 giá trị




Chọn A.