

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Chọn đáp án A
+ Để diện tích ABCD nhỏ nhất thì C và D phải nằm trên hai cực đại ngoài cùng.
Xét các đường cực đại ta có: ![]()
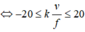
![]()
![]()
Vậy D nằm trên cực đại ứng với ![]()
Tam giác ABD vuông tại A nên ta có:
![]()
![]()
![]()
![]()

Đáp án B
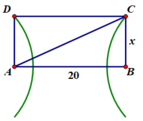
Để S hình chữ nhật ABCD nhỏ nhất và C, D đều nằm trên đường cực đại thì C và D phải nằm trên 2 đường cực đại gần nguồn nhất.
Có
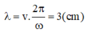
Số đường cực đại trên AB:
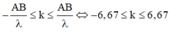
Để C là cực đại gần nguồn nhất thì k = 6.
Suy ra
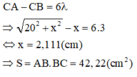

+ Bước sóng:
![]()
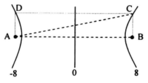
+ Diện tích nhỏ nhất khi C và D gần AB nhất.
+ vậy C và D phải thuộc hai cực đại ngoài cùng của AB.
+ Số cực đại trên AB được xác định bởi:

+ vậy diện tích hình chữ nhật ABCD nhỏ nhất là:
![]()
=> Chọn C.

Đáp án B
Ta có :
![]()
Trên AB , dao động cực đại gần A ( hoặc B ) nhất là :
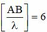
Để điện tích hình chữ nhật nhỏ nhất , CD nằm trên cực đại ứng với k = 6 và k = -6
Tại điểm D :
![]()
![]()
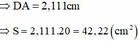

Đáp án A
Vì AB không đổi nên để diện tích HCN ABCD min thì BC phải min, tức là C phải là cực đại gần B nhất. Có λ = 3 cm.


Đáp án B
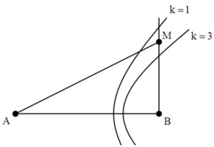
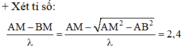
Vậy để N là một cực đại trên By và gần M nhất thì N chỉ có thể thuộc hypebol ứng với k = 3 hoặc k = 1.
+ Với k = 1, ta có:
