Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
$y'=\frac{-1}{(x+1)^2}$
Giao điểm của đồ thị $y=\frac{x+2}{x+1}$ vớ trục hoành là $(-2,0)$
PTTT của $y=\frac{x+2}{x+1}$ tại điểm tiếp điểm $(-2,0)$ là:
$y=f'(-2)(x+2)+f(-2)=\frac{-1}{(-2+1)^2}(x+2)+0$
$y=-x-2$
Đường tiếp tuyến $y=-x-2$ cắt trục tung tại điểm có tung độ:
$y=-0-2=-2$

Chọn C
Phương trình hoành độ giao điểm của hai đồ thị hàm số là: sinx = cosx

Vậy đồ thị hai hàm số đã cho cắt nhau tại 5 điểm trên đoạn - 2 π ; 5 π 2

- Tập xác định: D = R\ {1}
- Đạo hàm: 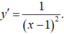
- Đồ thị hàm số cắt trục hoành tại 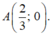
- Hệ số góc của tiếp tuyến tại A là 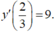
Chọn A.

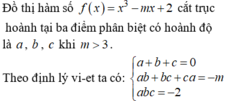

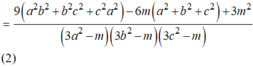
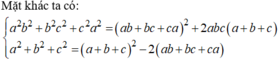
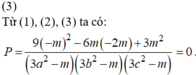
y=cosx cắt trục hoành khi y=0
=>\(cosx=0\)
=>\(x=\dfrac{\Omega}{2}+k\Omega\)
\(x\in\left(-\dfrac{3}{2}\Omega;\dfrac{3}{2}\Omega\right)\)
=>\(\dfrac{\Omega}{2}+k\Omega\in\left(-\dfrac{3}{2}\Omega;\dfrac{3}{2}\Omega\right)\)
=>\(k+\dfrac{1}{2}\in\left(-\dfrac{3}{2};\dfrac{3}{2}\right)\)
=>\(k\in\left(-2;1\right)\)
mà k nguyên
nên \(k\in\left\{-1;0\right\}\)
=>Đồ thị cắt trục Ox tại 2 điểm