Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

c, KE=KC mà góc CKE=90 =>góc KCE = 45 => góc KAB = 45 =>tam giác AKB vuông cân tại K =>K là điểm chính giữa cung AB
Giả sử KO cắt đương tròn tại P =>KP là đường kính và PK vuông góc với AB tại O
Ta có tam giác PBK vuông cân tại B =>PB=BK =>sđo cung PB = sđo cung BK mà sđo cung MB= sđo cung BN => sđo Cung PM= sđo cung KN =>PM=KN
=> KM^2 + KN^2 = KM^2 + PM^2 = PK^2 = AB^2 không đổi

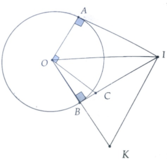
a, Chứng minh C là trực tâm của tam giác OIK. Từ đó suy ra KC ⊥ OI tại H
b, IA=12cm
Chứng minh ΔKOI cân tại K
Đặt KO = KI = x (x>0)
Có I K 2 = I B 2 + B K 2
Hay x 2 = 12 2 + x - 9 2
=> x = 12,5 => IK = 12,5cm