Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(C^2_{10}\) cách chọn hai quyển từ tầng \(k,k=1,2,3,4\). Vậy có tất cả \(\left(C^2_{10}\right)^4\) cách chọn
b) Tương tự, có \(\left(C^8_{10}\right)^4=\left(C^2_{10}\right)^4\) cách chọn

Lời giải:
Chọn 4 quyển sách khác nhau đủ 3 loại, có các TH sau:
TH1: 1 toán, 1 lý, 2 hóa: $A_1=C^1_6.C^1_7.C^2_8$ cách
TH2: 2 toán, 1 lý, 1 hóa: $A_2=C^2_6.C^1_7.C^1_8$ cách
TH3: 1 toán, 2 lý, 1 hóa: $A_3=C^1_6.C^2_7.C^1_8$ cách
Tổng số cách: $A_1+A_2+A_3=3024$ cách

Xếp theo thứ tự: ngữ văn- toán- ngữ văn- toán- ngữ văn- toán-ngữ văn-toán- ngữ văn. Vậy có 5.4.4.3.3.2.2.1=2880 cách
Chọn B

a) Có 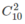 cách chọn hai quyển từ tầng thứ k, k = 1, 2, 3, 4
cách chọn hai quyển từ tầng thứ k, k = 1, 2, 3, 4
Vậy có tất cả 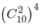 cách chọn.
cách chọn.
b) Tương tự, có 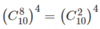 cách chọn.
cách chọn.

c. Số cách chọn 2 quyển sách khác môn học là: 5×6+5×8+6×8=118
Chọn C

a, Có \(C^2_9=36\) cách chọn 2 cuốn sách.
b, TH1: 1 quyển sách toán và 1 quyển sách văn.
Có 4 cách chọn sách toán.
Có 3 cách chọn sách văn.
\(\Rightarrow\) Có \(4.3=12\) cách chọn thỏa mãn.
TH2: 1 quyển sách toán và 1 quyển sách ngoại ngữ.
Có 4 cách chọn sách toán.
Có 2 cách chọn sách ngoại ngữ.
\(\Rightarrow\) Có \(4.2=8\) cách chọn thỏa mãn.
TH3: 1 quyển sách văn và 1 quyển sách ngoại ngữ.
Có 3 cách chọn sách văn.
Có 2 cách chọn sách ngoại ngữ.
\(\Rightarrow\) Có \(3.2=6\) cách chọn thỏa mãn.
Vậy có \(12+8+6=26\) cách chọn thỏa mãn yêu cầu bài toán.