Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

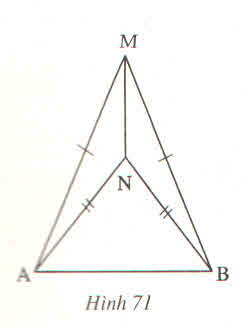
Xét tg AMN và tg BMN có:
MN chung
MA = MB (gt)
NA = NB (gt)
=> tg AMN = tg BMN (c.c.c)
1) Giả thiết: \(\Delta AMN;\Delta BMN\) có: MA = MB và NA = NB.
Kết luận: tg AMN = tg BMN
2) \(\Delta AMN\) và \(\Delta BMN\) có:
MN: cạnh chung
MA = MB (giả thiết)
NA = NB (giả thiết)
Do đó \(\Delta AMN=\Delta BMN\left(c.c.c\right)\)
Suy ra \(\widehat{AMN}=\widehat{BMN}\) (2 góc t/ư).
bạn làm sai chỗ Kết luận: tg AMN = tg BMN VÌ ngta nói chứng minh góc chứ ko phải tg

A B C N M y x 1 2 1
a) Vì AM là phân giác của góc BAM
=> Góc A1 = góc A2
Mà góc A1 = góc M1 ( do AB // MN )
=> Góc A2 = góc M1 ( điều phải c/m )
b) Vì Bx là phân giác góc ABC => Góc NBM = 1/2 góc ABC
Vì My là p/g của góc NMC => Góc yMC = 1/2 góc NMC
Mà góc NMC = góc ABC ( do AB // MN )
=> Điều phải c/m
c) Bn tự làm nốt nha

a: Xét ΔOMA và ΔOMB có
OM chung
MA=MB
OA=OB
Do đó: ΔOMA=ΔOMB
Xét ΔONA và ΔONB có
ON chung
NA=NB
OA=OB
Do đó: ΔONA=ΔONB
b: Ta có: OA=OB
nen O nằm tren đường trung trực của AB(1)
Ta có: MA=MB
nen M nằm trên đường trung trực của AB(2)
Ta có: NA=NB
nên N nằm trên đường trung trực của AB(3)
TỪ (1), (2)và (3) suy ra O,M,N thẳng hàng
c: Xét ΔAMN và ΔBMN có
AM=BM
MN chung
AN=BN
Do đó ΔAMN=ΔBMN
Chọn D