Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(v_{tb}=\dfrac{s}{t}=\dfrac{s'+s''}{t}=\dfrac{v'.t'+v''.t''}{t}=\dfrac{v'\dfrac{t}{2}+v''\dfrac{t}{2}}{t}\)\(\Leftrightarrow45=\dfrac{50\dfrac{t}{2}+v''\dfrac{t}{2}}{t}\)
\(\Rightarrow v''=40\left(\dfrac{km}{h}\right)\)

14/2 thời gian đã đi là 1/2 thời gian dự định hay 1/2 thời gian đi 1/3 đoạn đường đầu?

bài 1:
tóm tắt
\(s=18km=18000m\)
\(t=30'=1800s\)\(=0,5h\)
\(v=?\)
giải
ADCT: \(v=\dfrac{s}{t}\); ta có:
vận tốc của ô tô theo đơn vị km/h là:
\(\dfrac{18}{0,5}=36\left(km/h\right)\)
vận tốc của ô tô theo đơn vị m/s là:
\(\dfrac{18000}{1800}=10\left(m/s\right)\)
bài 2:
tóm tắt
\(s=9000m=9km\)
\(v=45km/h\)
\(t=?\)
giải:
ADCT: \(v=\dfrac{s}{t}\Rightarrow t=\dfrac{s}{v}\); ta có:
thời gian mà xe máy di chuyển hết quãng đường AB là:
\(\dfrac{9}{45}=\dfrac{1}{5}=0,2\left(h\right)\)

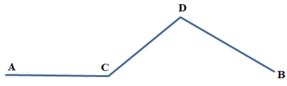
Lần lượt tính vận tốc xe leo dốc: v2 = 1/3.v1 = 15km/h.
Vận tốc xuống dốc: v3 = 4.v2 = 60 km/h
Quãng đường trên từng chặng đường là:
Chặng đường bằng AC: S1 = v1.t1 = 45.1/3 = 15 km
Chặng lên dốc CD: S2 = v2.t2 = 15.1/2 = 7,5 km
Chặng xuống dốc DB: S3 = v3.t3 = 60.1/6 = 10 km
Độ dài chặng đường: S = s1 + s2 + s3 = 32,5 km

mÌNH MỎI TAY QUÁ
Lấy gốc tọa độ tại AA chiều dương là chiều từ AA đến BB. Gốc thời gian là lúc 7h7h
Phương trình chuyển động của :
Xe đi từ A:A: xA=36t(km−h)xA=36t(km−h)
Xe đi từ B:xB=96−28t(km−h)B:xB=96−28t(km−h)
Hai xe gặp nhau khi :xA=xB:xA=xB
→36t=96−28t→36t=96−28t
⇒t=1,5(h)⇒t=1,5(h)
xA=36t=36.1,5=54(km)xA=36t=36.1,5=54(km)
Hai xe gặp nhau lúc 8h30′8h30′. Nơi gặp nhau cách AA 54km54km
TH1:TH1: Hai xe cách nhau 24km24km trước khi hai xe gặp nhau
Hai xe cách nhau 24km
⇔⇔ xB−xA=24xB−xA=24
⇔⇔ 96−28t′−36t′=2496−28t′−36t′=24
⇔t′=1,125h⇔t′=1,125h
Vậy lúc 8h7phút30giây hai xe cách nhau 24km
TH2:TH2: Hai xe cách nhau 24k sau khi gặp nhau
Hai xe cách nhau 24km
⇔xA−xB=24⇔xA−xB=24
⇔36t′′−96+28t′′=24⇔36t″−96+28t″=24
⇔t′′=1,875(h)⇔t″=1,875(h)
Vậy lúc 8h52phút30giây hai xe cách nhau 24km
bài 2:
ta có:
thời gian người đó đi trên nửa quãng đường đầu là:
t1=S1/v1=S/2v1=S/24
thời gian người đó đi hết nửa đoạn quãng đường cuối là:
t2=S2/v2=S2/v2=S/40
vận tốc trung bình của người đó là:
vtb=S/t1+t2=S/(S/40+S/24)=S/S(140+124)=1/(1/24+1/40)
⇒vtb=15⇒vtb=15 km/h
bài 3:
thời gian đi nửa quãng đầu t1=(1/2) S.1/25=S/50
nửa quãng sau (1/2) t2.18+(1/2) t2.12=(1/2) S⇔t2=S/30
vận tốc trung bình vtb=S/(t1+t2)=S/S.(1/50+1/30)=1/(1/50+1/30)=18,75(km/h)
HT

a) Xe đến B trước là xe 1.
Thời gian xe 1 đi: 54;50 = 1.08 (giờ)
Thời gian xe 2 đi là: \(\dfrac{54;3}{60}\) + \(\dfrac{54-\left(54;3\right)}{45}\) = 0.3 + 0.8 = 1.1 (giờ)
1.8 < 1.1 suy ra xe 1 đến B trước.
b) Khi hai xe gặp nhau, tức là chúng đã đi được quãng đường bằng nhau kể từ A.
Gọi t là thời gian từ lúc hai xe bắt đầu xuất phát đến khi gặp nhau; ta có phương trình:
50t = \(\dfrac{54}{3}\)+ 45(t - \(\dfrac{54:3}{60}\))
5t = 4.5
t = 0.9 (giờ)
Suy ra, vị trí hai xe gặp nhau cách A: 0.9 x 50 = 45 (km)
![]() chúc em học vui nha!
chúc em học vui nha!
a/ Thời gian đi hết đoạn đường AB :
\(t=\dfrac{s}{v}=\dfrac{45}{30}=1,5\left(h\right)\)
b/ Để đến AB sớm hơn 30p ô tô phải đi với thời gian là \(1h\)
Vận tốc ô tô cần đi khi đó :
\(v'=\dfrac{s}{t'}=\dfrac{45}{1}=45\left(km\backslash h\right)\)