Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Số tam giác là \(C_{2n}^3\). Một đa giác đều 2n đỉnh thì có n đường chéo xuyên tâm. Cứ 2 đường chéo xuyên tâm thì có một hình chữ nhật theo yêu cầu. Vậy số hình chữ nhật là \(C_n^2\).
Theo bài ta có phương trình :
\(C_{2n}^3=20C_n^2,\left(n\ge2\right)\)
\(\Leftrightarrow\frac{\left(2n\right)!}{\left(2n-3\right)!3!}=20\frac{n!}{\left(n-2\right)!2!}\)
\(\Leftrightarrow\frac{\left(2n-2\right)\left(2n-1\right)2n}{3}=20\left(n-1\right)n\)
\(\Leftrightarrow2\left(n-1\right)\left(2n-1\right)2n=60\left(n-1\right)n\)
\(\Leftrightarrow2n-1=15\), (do \(n\ge2\))
\(\Leftrightarrow n=18\)
Vậy đa giác đều có 16 cạnh, (thập lục giác đều)

- a) \(m = \left(\right. A D M \left.\right) \cap \left(\right. A B N \left.\right)\) là đường thẳng duy nhất đi qua \(A\) nằm trong cả hai mặt phẳng. (Dựng được bằng cách lấy một mặt phẳng phụ \(\pi\) qua \(A\) và lấy giao tuyến \(\pi \cap \left(\right. A D M \left.\right)\) và \(\pi \cap \left(\right. A B N \left.\right)\).)
- b) Với \(P \in m\) (nội tiếp tứ diện), đặt \(Q = M P \cap \left(\right. A D C \left.\right)\). Khi đó \(\left(\right. M N P \left.\right) \cap \left(\right. A D C \left.\right) = N Q\).

(la) A E D B C G F c b
Đặt \(\overrightarrow{AB}=\overrightarrow{b,}\overrightarrow{AC}=\overrightarrow{c,}t=\frac{BF}{FC}\)
Khi đó, \(\overrightarrow{AE}=p,\overrightarrow{AD}=q\overrightarrow{c},p,q\in\left(0;1\right)\) và
\(\overrightarrow{AF}=\frac{t\overrightarrow{c}+\overrightarrow{b}}{1+t};\overrightarrow{AG}=\frac{t\overrightarrow{AD}+\overrightarrow{AE}}{1+t}=\frac{tq\overrightarrow{c}+p\overrightarrow{b}}{1+t}\)
Mặt khác, do BE = tCD suy a \(\left(1-p\right)\left|b\right|=t\left(1-q\right)\left|\overrightarrow{c}\right|\)
Từ đó, với chú ý đường phân giác \(l_a\) có vec tơ chỉ phương là \(\frac{\overrightarrow{c}}{\left|\overrightarrow{c}\right|}+\frac{\overrightarrow{b}}{\left|\overrightarrow{b}\right|}\)
Suy ra :
\(\overrightarrow{GF}=\overrightarrow{AF}-\overrightarrow{AG}=\frac{t\overrightarrow{c}+\overrightarrow{b}}{1+t}-\frac{tq\overrightarrow{c}+p\overrightarrow{b}}{1+t}\)
\(=\frac{t\left(1-q\right)}{1+t}.\overrightarrow{c}+\frac{1-p}{1+t}.\overrightarrow{b}\)
\(=\frac{\left(1-q\right)\left|b\right|}{1+t\overrightarrow{ }}\left(\frac{\overrightarrow{c}}{\left|\overrightarrow{c}\right|}+\frac{\overrightarrow{b}}{\left|\overrightarrow{b}\right|}\right)=\frac{\left(1-q\right)\left|\overrightarrow{b}\right|}{1+t}.\overrightarrow{AL}\)
=> Điều phải chứng minh
Từ giả thiết suy ra với mọi điểm O đều có :
\(\overrightarrow{OP}=\frac{1}{2}\left(\overrightarrow{OB}+\overrightarrow{OC}\right)\), \(\overrightarrow{ON}=\frac{1}{2}\left(\overrightarrow{OA}+\overrightarrow{OE}\right)\Rightarrow\overrightarrow{OI}=\frac{1}{4}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OE}\right)\)
\(\overrightarrow{OM}=\frac{1}{2}\left(\overrightarrow{OA}+\overrightarrow{OB}\right)\), \(\overrightarrow{OQ}=\frac{1}{2}\left(\overrightarrow{OD}+\overrightarrow{OE}\right)\Rightarrow\overrightarrow{OJ}=\frac{1}{4}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OD}+\overrightarrow{OE}\right)\)
Từ đó suy ra \(\overrightarrow{JI}=\frac{1}{4}\left(\overrightarrow{OC}-\overrightarrow{OD}\right)\Rightarrow\) IJ // CD => Điều phải chứng minh

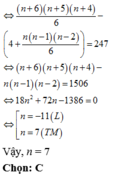


Chọn B
Lấy ba điểm phân biệt không thẳng hàng sẽ tạo thành một tam giác nên số tam giác tạo thành là: