Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

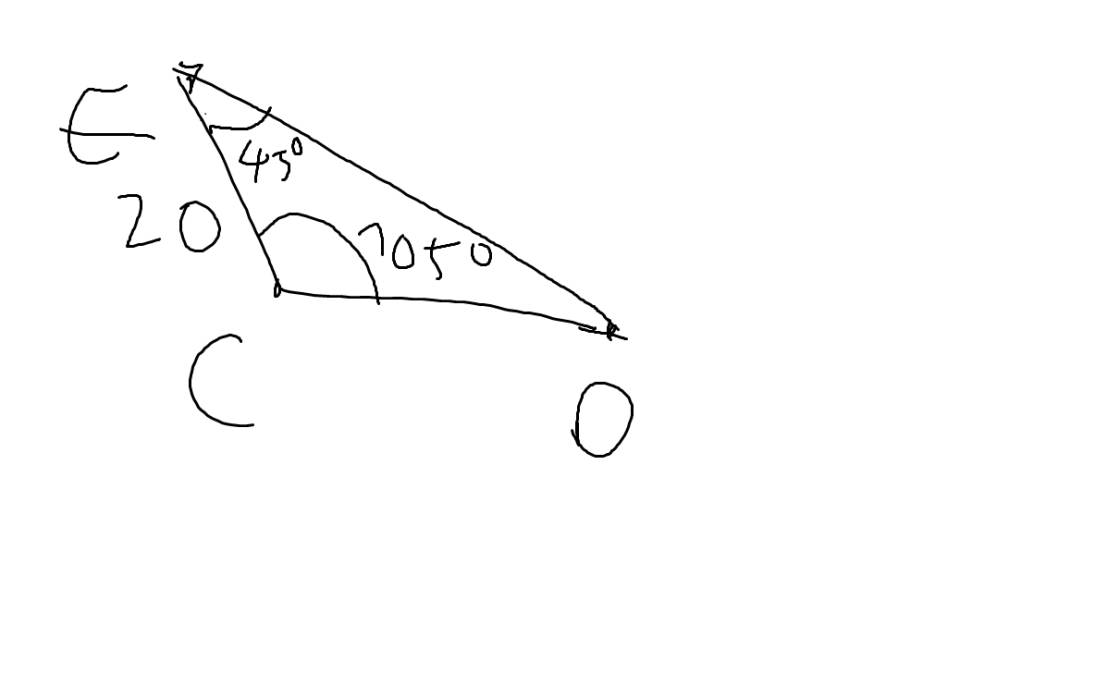
Xét ΔCED có \(\widehat{C}+\widehat{D}+\widehat{E}=180^0\)
=>\(\widehat{D}+105^0+45^0=180^0\)
=>\(\widehat{D}=30^0\)
Xét ΔCED có \(\dfrac{CE}{sinD}=\dfrac{CD}{sinE}\)
=>\(\dfrac{CD}{sin45}=\dfrac{20}{sin30}\)
=>\(\dfrac{CD}{sin45}=\dfrac{20}{\dfrac{1}{2}}=40\)
=>\(CD=40\cdot sin45=40\cdot\dfrac{\sqrt{2}}{2}=20\sqrt{2}\)

O O' A B H C F D K G E 1 2 3 4
a) Xét đường tròn (O';R) có: Đường kính OC và điểm A nằm trên cung OC => ^OAC=900
=> OA vuông góc với AC. Mà OA là bán kính của (O) => AC là tiếp tuyến của (O)
Ta thấy: 2 đường tròn (O) và (O') có cùng bán kính R => OA=OB=O'A=O'B= R
=> Tứ giác AOBO' là hình thoi =>OA // O'B
Lại có: OA vuông góc AC (cmt) => O'B vuông góc AC (Qhệ //, vg góc) hay BF vuông góc AC (đpcm).
b) Xét tứ giác ADKO: ^DKO=^OAD=900 (=^OAC)
=> Tứ giác ADKO nội tiếp đường tròn tâm là trg điểm OD (đpcm).
c) Do tứ giác AOBO' là hình thoi nên AB vuông góc OO' (tại H) (1)
Ta có điểm B thuộc (O') và F đối xứng B qua O' => F thuộc (O') (Vì đường tròn có tâm đối xứng)
Xét (O') đường kính BF và A thuộc cung BF => AB vuông góc AF (2)
Từ (1) và (2) => OO' // AF
Xét tứ giác AOO'F: OO' // AF; OA // O'F (cmt) => Tứ giác AOO'F là hình bình hành
=> AF = OO'. Mà AF=AD nên AD=OO'. Lại có: OO' = OA => AD=OA.
Xét tứ giác ADKO nội tiếp đường tròn => ^AOK+^ADK = 1800
Mà ^ADK + ^ADG = 1800 nên ^AOK=^ADG hay ^AOH=^ADG
Xét \(\Delta\)AHO và \(\Delta\)AGD: AO=AD (cmt); ^AOH=^ADG; ^AHO=^AGD=900
=> \(\Delta\)AHO=\(\Delta\)AGD (Cạnh huyền góc nhọn) => AH=AG
Xét tứ giác AHKG: ^AHK=^HKG=^HAG=900; AH=AG (cmt) => Tứ giác AHKG là hình vuông.
d) Dễ thấy: AO=OO'=O'A => Tam giác AOO' đều => ^AO'O = 600
Lại có: Hình bình hành AOO'F có O'O=O'F => Tứ giác AOO'F là hình thoi
=> ^AO'O=^AO'F = 600 => ^FO'C = 600
=> SHình quạt AO'O = 1/6 S (O) = \(\frac{R^2.\pi}{6}\)
Tương tự, suy ra: S H.quạt AO'O = S H.quạt BO'O = S H,quạt AOO' = S H.quạt BOO' = \(\frac{R^2.\pi}{6}\)
Cộng tất cả lại => \(S_1+S_2+S_3+S_4+2.S_{AOBO'}=4.\frac{R^2.\pi}{6}=\frac{2R^2.\pi}{3}\)
\(\Rightarrow S_1+S_2+S_3+S_4+S_{AOBO'}=\frac{2R^2.\pi}{3}-S_{AOBO'}\)
\(\Rightarrow S_{P.C}=\frac{2R^2.\pi}{3}-R^2.\frac{\sqrt{3}}{2}=\frac{4R^2.\pi}{6}-\frac{3\sqrt{3}.R^2}{6}=\frac{R^2.\left(4\pi-3\sqrt{3}\right)}{6}\)
\(=\frac{R^2.\left(4.3,14-3.1,73\right)}{6}=\frac{R^2.7,37}{6}\)(Chú thích SPhần chung: SP.C)
Vậy diện tích phần chung của (O0 và (O') tính theo R là \(S_{P.C}=\frac{7,37.R^2}{6}.\)
F G A B C E O' K D N O
a) Xét đường tâm O'
\(\widehat{OAC}=90^o\)

ˆBAD=900+12002=1050BAD^=900+12002=1050 (góc nội tiếp chắn cung BCD) (1)
ˆADC=600+9002=750ADC^=600+9002=750 ( góc nội tiếp chắn cung ABC) (2)
Từ (1) và (2) có:
ˆBAD+ˆADC=1050+750=1800BAD^+ADC^=1050+750=1800 (3)
ˆBADBAD^ và ˆADCADC^ là hai góc trong cùng phía tạo bởi cát tuyến AD và hai đường thẳng AB, CD.
Đẳng thức (3) chứng tỏ AB // CD. Do đó tứ giác ABCD là hình thang, mà hình thang nội tiếp là hình thang cân.
Vậy ABCD là hình thang cân (BC = AD và sđ cung BC = AD = 90o )
b) Giả sử hai đường chéo AC và BD cắt nhau tại I.
ˆCIDCID^ là góc có đỉnh nằm trong đường tròn, nên:
ˆCID=sđcungAB+sđcungCD2=600+12002=900CID^=sđcungAB+sđcungCD2=600+12002=900
Vậy AC ⊥ BD
c)
Vì sđ cung AB = 60o nên ˆAIB=600AIB^=600 => ∆AIB đều, nên AB = R
Vì sđ cung BC = 90o nên BC = R√2
AD = BC = R√2
nên sđ cung CD= 120o nên CD = R√3
Hướng dẫn giải:
ˆBAD=900+12002=1050BAD^=900+12002=1050 (góc nội tiếp chắn cung BCD) (1)
ˆADC=600+9002=750ADC^=600+9002=750 ( góc nội tiếp chắn cung ABC) (2)
Từ (1) và (2) có:
ˆBAD+ˆADC=1050+750=1800BAD^+ADC^=1050+750=1800 (3)
ˆBADBAD^ và ˆADCADC^ là hai góc trong cùng phía tạo bởi cát tuyến AD và hai đường thẳng AB, CD.
Đẳng thức (3) chứng tỏ AB // CD. Do đó tứ giác ABCD là hình thang, mà hình thang nội tiếp là hình thang cân.
Vậy ABCD là hình thang cân (BC = AD và sđ cung BC = AD = 90o )
b) Giả sử hai đường chéo AC và BD cắt nhau tại I.
ˆCIDCID^ là góc có đỉnh nằm trong đường tròn, nên:
ˆCID=sđcungAB+sđcungCD2=600+12002=900CID^=sđcungAB+sđcungCD2=600+12002=900
Vậy AC ⊥ BD
c)
Vì sđ cung AB = 60o nên ˆAIB=600AIB^=600 => ∆AIB đều, nên AB = R
Vì sđ cung BC = 90o nên BC = R√2
AD = BC = R√2
nên sđ cung CD= 120o nên CD = R√3

Sửa đề : I là trung điểm AO
O A B x y I M E F
a,Xét tứ giác AEIM có ^EAI + ^EMI = 90o
=> Tứ giác AEIM nội tiếp
Tương tự tứ giác MIBF nội tiếp
b,Vì tứ giác AEIM nội tiếp
=> ^MEI = ^MAI
Tương tự ^MFI = ^MBI
Vì M thuộc (O) đường kính AB
=> ^AMB = 90o
=> ^MAI + ^MBI = 90o
=> ^MEI + ^MFI = 90o
=> ^EIF = 90o
c, Xét \(\Delta\)AEI và \(\Delta\)BIF có
^EAI = ^FBI ( = 90o )
^AEI = ^BIF (Cùng phụ ^EIA)
\(\Rightarrow\Delta AEI\approx\Delta BIF\left(g.g\right)\)
=> AE . BF = AI . BI
Vì I là trung điểm AO
=> \(AI=\frac{AO}{2}=\frac{R}{2}\)
=> \(BI=AB-AI=2R-\frac{R}{2}=\frac{3R}{2}\)
\(\Rightarrow AE.BF=AI.BI=\frac{R}{2}.\frac{3R}{2}=\frac{3R^2}{4}\)
d,(Mấy cái lặt vặt tính cạnh theo R mình không làm nữa nhé , bạn tự hiểu nha)
Có \(S_{EIF}=S_{AEBF}-S_{AEI}-S_{BIF}\)
\(=\frac{\left(AE+BF\right).AB}{2}-\frac{AE.AI}{2}-\frac{BI.BF}{2}\)
\(=\frac{\left(AE+BF\right).2R}{2}-\frac{AE}{2}.\frac{R}{2}-\frac{BF}{2}.\frac{3R}{2}\)
\(=\left(AE+BF\right).R-\frac{AE.R}{4}-\frac{3BF.R}{4}\)
\(=AE.R-\frac{AE.R}{4}+BF.R-\frac{3BF.R}{4}\)
\(=\frac{3AE.R}{4}+\frac{BF.R}{4}\)
\(\ge2\sqrt{\frac{3AE.R.BF.R}{4.4}}\)
\(=2\sqrt{\frac{3R^2.AE.BF}{16}}\)
\(=2\sqrt{\frac{3R^2.\frac{3R^2}{4}}{16}}\)
\(=\frac{3R^2}{4}\)
Dấu "=" xảy ra \(\Leftrightarrow\frac{3AE.R}{4}=\frac{BF.R}{4}\)
\(\Leftrightarrow3AE=BF\)
Thay vào \(AE.BF=\frac{3R^2}{4}\)
\(\Leftrightarrow AE.3AE=\frac{3R^2}{4}\)
\(\Leftrightarrow AE=\frac{R}{2}\)
\(\Leftrightarrow BF=\frac{3R}{2}\)
Vậy .,..........

Tham khảo bài làm của một số bạn ở đây nhé :
Bài 42 Sgk tâp 1 - trang 96 - Toán lớp 9 | Học trực tuyến
Bây giờ đăng toàn mất link thôi , vào thống kê hỏi đáp của mình nhé : )
46,23m
Trên bờ bên kia của dòng sông lấy điểm B, bờ bên này lấy điểm A đối diện với B. Để đo gián tiếp độ rộng của dòng sông (khoảng cách AB), người ta lấy điểm C bên này sông và cách A một khoảng AC = 80 mét, đặt giác kế tại C và đo được góc ^ACB = 34o. Tính chiều rộng AB của con sông?
( Cho biết: sin34o = 0,56 ; cos34o = 0,83 ; tg34o = 0,67 ; cotg34o = 1,48 )