Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chiều dài một vòng của quỹ đạo là : \(9000.2.\pi \) (km)
Quãng đường vệ tinh đã chuyển động được sau 1 giờ là \(\frac{{9000.2.\pi }}{3} = 6000\pi \)(km)
Quãng đường vệ tinh đã chuyển động được sau 3 giờ là \(18000\pi \)(km)
Quãng đường vệ tinh đã chuyển động được sau 5 giờ là \(\frac{{9000.2.\pi }}{3}.5 = 30000\pi \)(km)
b)Vệ tinh chuyển động được quãng đường 200 000 km sau sô giờ là : \(\frac{{200000}}{{6000\pi }} \approx 11\)(giờ)

tham khảo:
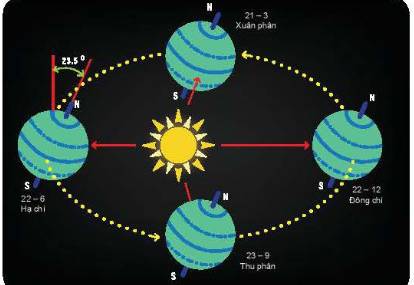
a) Vì trục quay của Trái Đất luôn cố định hướng về một phương cố định trong không gian, và mặt phẳng quỹ đạo cũng không thay đổi trong quá trình quay quanh Mặt Trời.
b) Trong quá trình chuyển động quanh Mặt Trời, hình chiếu của trục Trái Đất trên mặt phẳng quỹ đạo sẽ thay đổi theo thời gian và tạo thành một đường tròn có bán kính bằng góc nghiêng của trục quay so với mặt phẳng quỹ đạo. Khi Trái Đất ở vị trí xa nhất (khoảng 4/7 quỹ đạo) và gần nhất (khoảng 3/7 quỹ đạo) so với Mặt Trời, thì hình chiếu của trục quay của Trái Đất trên mặt phẳng quỹ đạo sẽ nằm trên đường thẳng nối tâm Trái Đất và Mặt Trời.

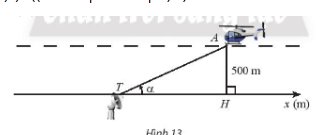
a, Xét tam giác AHT vuông tại H, ta có:
\(cot\alpha=\dfrac{TH}{AH}\Rightarrow TH=AH\cdot cot\alpha=500\cdot cot\alpha\)
Vậy trên trục \(T_x\) tọa độ \(x_H=500\cdot cot\alpha\)
b, Ta có đồ thị của hàm số \(y=cot\alpha\) trong khoảng \(\dfrac{\pi}{6}< \alpha< \dfrac{2\pi}{3}\)
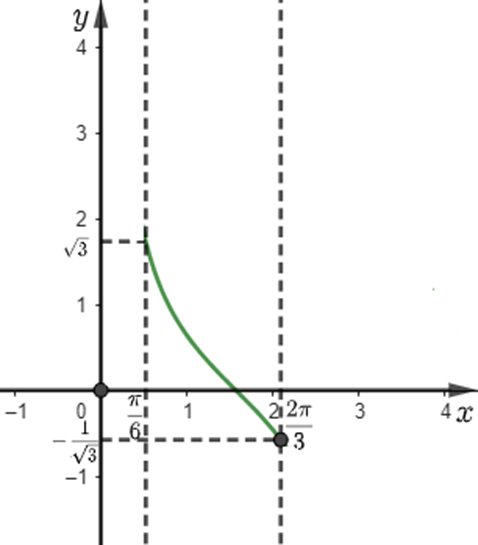
Khi đó:
\(-\dfrac{1}{\sqrt{3}}< cot\alpha< \dfrac{1}{\sqrt{3}}\Leftrightarrow-\dfrac{500}{\sqrt{3}}< 500\cdot cot\alpha< \dfrac{500}{\sqrt{3}}\\ \Leftrightarrow-\dfrac{500}{\sqrt{3}}< x_H< \dfrac{500}{\sqrt{3}}\\ \Leftrightarrow-288,7< x_H< 866\)
Vậy \(x\in\left\{-288,7;866\right\}\)

Số năm Trái Đất để sao Hỏa quay quanh mặt trời là:
\(P=d^{\dfrac{3}{2}}=1.52^{1,5}\simeq1,87\left(AU\right)\)

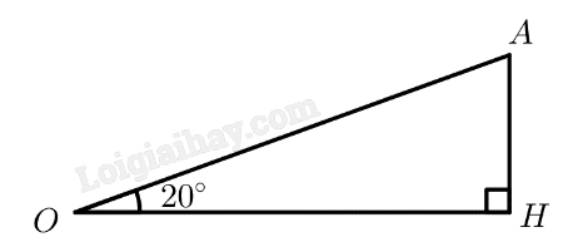
Đổi \(200km/h = \frac{{500}}{9}m/s\)
Mô hình hoá như hình vẽ, với \(OA\) là quãng đường máy bay bay được sau 2 giây, \(OH\) là độ cao của máy bay so với mặt đấy khi máy bay bay được sau 2 giây, độ lớn của góc \(\widehat {AOH}\) chỉ số đo góc giữa máy bay với mặt đất.
Sau 2 giây máy bay bay được quãng đường là: \(\frac{{500}}{9}.2 = \frac{{1000}}{9}\left( m \right)\)
Vì tam giác \(OAH\) vuông tại \(H\) nên ta có:
\(AH = OA.\sin \widehat {AOH} = \frac{{1000}}{9}.\sin {20^ \circ } \approx 38,0\left( m \right)\)
Vậy độ cao của máy bay so với mặt đất là 38 mét sau khi máy bay rời khỏi mặt đất 2 giây.

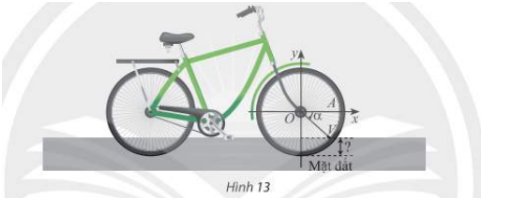
Sau một phút di chuyển, van V đã quay được một góc lượng giác có số đo góc là: \(\alpha=11\cdot60=660\left(rad\right)\)
Khi đó tọa độ điểm V biểu diễn cho góc lượng giác trên có tọa độ là: \(V\left(58\cdot cos\alpha,58\cdot sin\alpha\right)\approx\left(56;15,2\right)\)
Từ đó, khoảng cách từ van đến mặt đất khoảng \(58-15,2\approx42,8\left(cm\right)\)

a)
\(\begin{array}{l}F = 0\;\\ \Rightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 0\;\; \Leftrightarrow 1 - \cos \alpha = 0\;\; \Leftrightarrow \cos \alpha = 1\; \Leftrightarrow \alpha = k2\pi \;\left( {k \in \mathbb{Z}} \right)\end{array}\)
b) \(F = 0,25\; \Rightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 0,25\; \Leftrightarrow 1 - \cos \alpha = \frac{1}{2}\;\; \Leftrightarrow \cos \alpha = \frac{1}{2}\; \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\alpha = \frac{\pi }{3} + k2\pi }\\{\alpha = - \frac{\pi }{3} + k2\pi }\end{array}\;\left( {k \in \mathbb{Z}} \right)} \right.\)
c) \(F = 0,5\;\; \Rightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 0,5\; \Leftrightarrow 1 - \cos \alpha = 1\; \Leftrightarrow \cos \alpha = 0\; \Leftrightarrow \alpha = \frac{\pi }{2} + k\pi \;\;\left( {k \in \mathbb{Z}} \right)\)
d) \(F = 1\; \Leftrightarrow \frac{1}{2}\left( {1 - \cos \alpha } \right) = 1\;\; \Leftrightarrow 1 - \cos \alpha = 2\; \Leftrightarrow \cos \alpha = - 1\; \Leftrightarrow \alpha = \pi + k2\pi \;\left( {k \in \mathbb{Z}} \right)\)

Chọn đáp án C
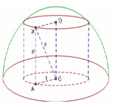
Hình trụ nội tiếp nửa mặt cầu, nên theo giả thiết đường tròn đáy trên có tâm O’ là hình chiếu của O xuống mặt đáy (O’). Suy ra hình trụ và nửa mặt cầu cùng chung trục đối xứng và tâm của đáy dưới hình trụ trùng với tâm O của nửa mặt cầu.
![]()
Thể tích khối trụ là
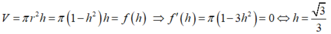
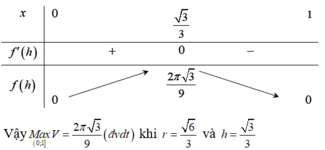

a)
x | \( - \pi \) | \( - \frac{{2\pi }}{3}\) | \[ - \frac{\pi }{2}\] | \( - \frac{\pi }{3}\) | 0 | \(\frac{\pi }{3}\) | \(\frac{\pi }{2}\) | \(\frac{{2\pi }}{3}\) | \(\pi \) |
\(y = \cos x\) | -1 | \( - \frac{1}{2}\) | 0 | \(\frac{1}{2}\) | 1 | \(\frac{1}{2}\) | 0 | \( - \frac{1}{2}\) | -1
|
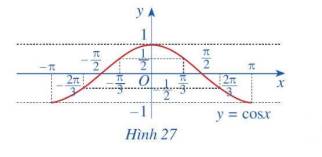
b) Trong mặt phẳng tọa độ Oxy, hãy biểu diễn các điểm (x; y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm \(\left( {x;\cos x} \right)\) với \(x \in \left[ { - \pi ;\pi } \right]\) và nối lại ta được đồ thị hàm số \(y = \cos x\) trên đoạn \(x \in \left[ { - \pi ;\pi } \right]\) (Hình 27)
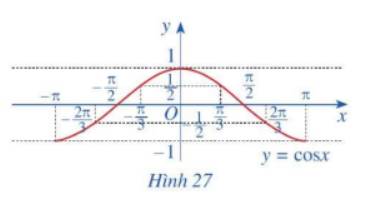
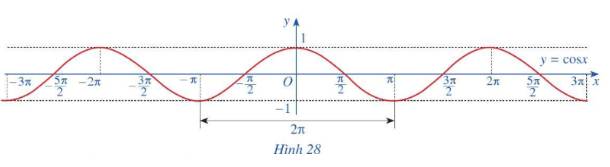
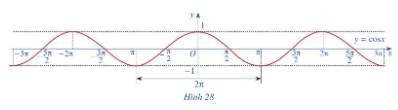
c) Làm tương tự như trên đối với các đoạn \(\left[ { - 3\pi ; - \pi } \right]\), \(\left[ {\pi ;3\pi } \right]\),...ta có đồ thị hàm số \(y = \cos x\)trên R được biểu diễn ở Hình 28.
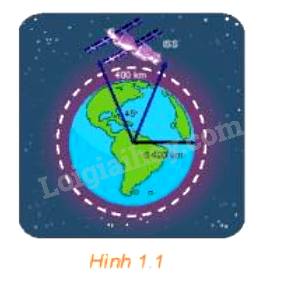


Bán kính quỹ đạo của trạm vũ trụ quốc tế là R = 6 400 + 400 = 6 800 (km).
Đổi \(45{}^\circ =45\cdot \frac{\pi }{180}=\frac{\pi }{4}\).
Vậy trong khi được trạm mặt đất theo dõi, trạm ISS đã di chuyển một quãng đường có độ dài là \(l = R\alpha \text{ = }6\,800\cdot \frac{\pi }{4}\approx 5\,340,708\approx 5\,341\,(km)\).