Tổng tất cả các nghiệm thực của phương trình 2 log 4 x

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn lớp

Chọn môn

Mua vip

Pham Trong Bach

25 tháng 9 2018

Tổng tất cả các nghiệm thực của phương trình 2 log 4 x - 3 + log 4 x - 5 2 = 0 là

#Toán lớp 12

Cao Minh Tâm

25 tháng 9 2018

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Pham Trong Bach

3 tháng 10 2018

Có tất cả bao nhiêu số nguyên m để phương trình log ( m - x ) = 3 log ( 4 - 2 x - 3 ) có hai nghiệm thực phân biệt

A. 6

B. 2

C. 3

D. 5

#Toán lớp 12

Cao Minh Tâm

3 tháng 10 2018

Đúng(0)

Phạm Trần Phát

17 tháng 12 2023

Câu 11: Nghiệm của phương trình $\log^2_{\frac{1}{2}} (x-2)-(2-x)\log_{2} (x-2)+3(x-5)=0$ là?

#Toán lớp 12

Pham Trong Bach

28 tháng 9 2018

Tìm số nghiệm nguyên của bất phương trình log 5 2 ( 3 x - 2 ) log 2 ( 4 - x ) - log ( 4 - x ) 2 + 1 > 0 A. 3 B. 1 C. 0 D....

Đọc tiếp

#Toán lớp 12

Cao Minh Tâm

28 tháng 9 2018

Đúng(0)

Minh Anh

19 tháng 4 2020

31. Tổng tất cả các nghiệm của phương trình log(8.5^x + 20^x ) = x + log 25 bằng ?

#Toán lớp 12

Akai Haruma

Giáo viên

19 tháng 4 2020

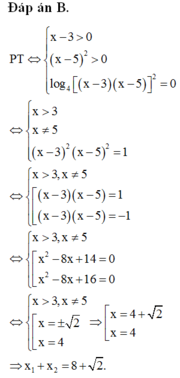
Lời giải:

$\log(8.5^x+20^x)=x+\log 25$

$\Rightarrow 8.5^x+20^x=10^{x+\log 25}=10^x.25$

$\Rightarrow \frac{8.5^x+20^x}{10^x}=25$

$\Leftrightarrow \frac{8}{2^x}+2^x=25$

Đặt $2^x=t$ thì $\frac{8}{t}+t=25$

$\Leftrightarrow t^2-25t+8=0$

Dễ thấy PT trên luôn có 2 nghiệm dương $t_1,t_2$ nên kéo theo PT ban đầu có 2 nghiệm $x_1,x_2$

Tổng các nghiệm $x_1+x_2=\log_2(t_1)+\log_2(t_2)=\log_2(t_1t_2)=\log_2(8)=3$

Đúng(0)

Nguyễn Tùng Anh

28 tháng 12 2021

Cho phương trình: $\left(x^2-1\right).log^2\left(x^2+1\right)-m\sqrt{2\left(x^2-1\right)}.log\left(x^2+1\right)+m+4=0$. Có bao nhiêu giá trị nguyên của tham số m thuộc [-10;10] để phương trình đã cho có 2 nghiệm phân biệt thỏa mãn $1\le|x|\le3$

#Toán lớp 12

Pham Trong Bach

15 tháng 11 2019

Tích các nghiệm của phương trình log 2 x + 2 - log x = 2 là A. 10 3 - 5 2 B. 10 3 + 2 2 C. 10 3 + 5 2 D. 10 3 - 2 2 ...

Đọc tiếp

#Toán lớp 12

Cao Minh Tâm

15 tháng 11 2019

Đúng(0)

Nguyễn Vi

4 tháng 6 2019

Tổng tất cả các nghiệm của phương trình log₅(6-5^x)=1-x bằng

#Toán lớp 12

Nguyễn Việt Lâm

Giáo viên

5 tháng 6 2019

ĐKXĐ: $6-5^x>0\Rightarrow5^x< 6$

$log_5\left(6-5^x\right)=1-x\Leftrightarrow6-5^x=5^{1-x}$

$\Leftrightarrow5^x-6+\frac{5}{5^x}=0\Leftrightarrow\left(5^x\right)^2-6.5^x+5=0$

$\Rightarrow\left[{}\begin{matrix}5^x=1\\5^x=5\end{matrix}\right.$ $\Rightarrow\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.$ $\Rightarrow\sum x=0+1=1$

Đúng(0)

Thái Thùy Linh

10 tháng 3 2021

Cho phương trình log²(10x) - 2mlog_10xx - log(10x²)=0 . Gọi S là tập chứa tất cả các giá trị nguyên của m thuộc [-10;10] để phương trình đã cho có đúng 3 nghiệm phân biệt . Số phần tử của tập S là

#Toán lớp 12