Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Ta có AC'=6 nên AB = 2 3 .
Mặt cầu (S) có tâm I(2;4;-1) trùng với tâm hình lập phương ABCD.A'B'C'D' và có bán kính R =1 < A B 2 nên mặt cầu (S) nằm trong hình lập phương ABCD.A'B'C'D'.
Với mọi điểm M nằm trong hình lập phương ABCD.A'B'C'D', tổng các khoảng cách từ điểm M đến 6 mặt của hình lập phương ABCD.A'B'C'D' bằng 3AB = 6 3 .
Vậy từ một điểm M bất kỳ thuộc mặt cầu (S), tổng các khoảng cách từ điểm M đến 6 mặt của hình lập phương ABCD.A'B'C'D' bằng 6 3 .

Gọi giao điểm của (α) với ba tia Ox, Oy, Oz lần lượt là A(a; 0; 0), B(0; b; 0), C(0; 0 ; c) (a, b, c > 0).
Mặt phẳng (α) có phương trình theo đoạn chắn là:
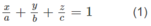
Do (α) đi qua M(1; 2; 3) nên ta thay tọa độ của điểm M vào (1):
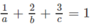
Thể tích của tứ diện OABC là:
![]()
Áp dụng bất đẳng thức Cô-si ta có:
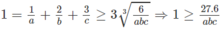
⇒ abc ≥ 27.6 ⇒ V ≥ 27
Ta có: V đạt giá trị nhỏ nhất ⇔ V = 27
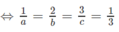
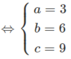
Vậy phương trình mặt phẳng ( α ) thỏa mãn đề bài là:
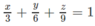
hay 6x + 3y + 2z – 18 = 0

Chọn D.
Dễ thấy A'A, B'M, D'N đồng quy tại S, SA' = 2a. Từ đó, ta tính được V S . A ' B ' D ' và V S . AMN . Suy ra tính được V H

Đáp án B
Khối lập phương có thể tích bằng 8 nên hình lập phương có cạnh bằng 2.
Hình lập phương có 6 mặt đều là hình vuông bằng nhau nên tổng diện tích cần tìm là 6. 22 = 24.
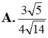
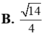
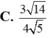
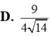

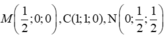
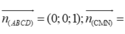
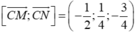
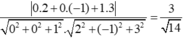
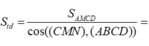
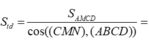
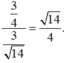
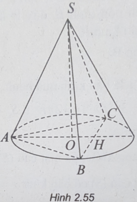
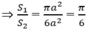
Chọn D