Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số cần tìm là \(\overline{ab}\left(a\inℕ^∗,a\le9;b\inℕ,b\le9\right)\)
Vì tổng hai chữ số bằng 8 nên ta có phương trình \(a+b=8\Leftrightarrow b=8-a\)(1)
Lại có \(\overline{ab}=10a+b\)
Khi viết chữ số 1 xen giữa 2 chữ số, ta được số mới là \(\overline{a1b}=100a+10+b\)
Số mới hơn số cũ 190 đơn vị nên ta có phương trình \(100a+10+b-\left(10a+b\right)=190\)
\(\Leftrightarrow90a=180\)\(\Leftrightarrow a=2\)(nhận)
Thay vào (1), ta có \(b=8-2=6\)(nhận)
Vậy số cần tìm là 26

Gọi chữ số hàng đơn vị là a thì chữ số hàng chục là a + 2
=> Số đó là (a+2)a = 10(a+2) + a = 11a + 20
Theo bài cho ta có:
11a + 20 = a2 + (a+2)2 + 1
<=> 11a + 20 = 2a2 + 4a + 5
<=> 2a2 - 7a -15 = 0
<=> 2a2 + 3a - 10a - 15 = 0
<=> a(2a + 3) - 5(2a + 3) = 0
<=> (a - 5)(2a + 3) = 0 <=> a = 5 hoặc a = -1,5 (Loại vì a là chữ số)
Vậy số đó là 75

Gọi x, y là hai số cần tìm.
Vì tổng của hai số bằng 59 nên ta có phương trình: x + y = 59
Vì hai lần của số này bé hơn ba lần của số kia là 7 nên ta có phương trình: 3y – 2x = 7.
Ta có hệ phương trình: 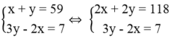
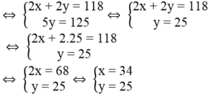
Vậy hai số cần tìm là 34 và 25

gọi số có 2 chữ số đó là: \(\overline{ab}\)
theo đề bài ta có:\(4a-b=17\Rightarrow b=4a-17\)
\(\overline{ab}-\overline{ba}=18\)
\(\Leftrightarrow10a+b-10b-a=18\)
\(\Leftrightarrow9a-9b=18\)
\(\Leftrightarrow a-b=2\)
\(\Leftrightarrow a-\left(4a-17\right)=2\)
\(\Rightarrow-3a=2-17\)
\(\Leftrightarrow-3a=-15\)
\(\Leftrightarrow a=5\)
ta lại có:\(4a-b=17\)
\(4\times5-b=17\)
\(b=3\)
vậy số cần tìm là \(53\)

Gọi hai số cần tìm là a,b
Tổng của hai số là 59 nên a+b=59(1)
Hai lần của số này bé hơn 3lần của số kia là 7 nên ta có:
3a-2b=7(2)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}a+b=59\\3a-2b=7\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+2b=118\\3a-2b=7\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5a=125\\a+b=59\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=25\\b=59-a=59-25=34\end{matrix}\right.\)
Vậy: Hai số cần tìm là 25 và 34

Gọi 2 số cần tìm là a và b ( \(a,b\inℕ^∗\))
Theo bài, ta có: \(\frac{a}{b}=\frac{4}{7}\)\(\Rightarrow\frac{a}{4}=\frac{b}{7}\)
Đặt \(\frac{a}{4}=\frac{b}{7}=k\left(k\inℕ^∗\right)\)\(\Rightarrow a=4k\); \(b=7k\)
Nếu lấy số thứ nhất chia cho 4, số thứ 2 chia cho 5 thì thương thứ nhất bé hơn thương thứ hai 2 đơn vị
\(\Rightarrow\)Ta có phương trình : \(\frac{7k}{5}-\frac{4k}{4}=2\)
\(\Leftrightarrow\frac{7k}{5}-k=2\)\(\Leftrightarrow\frac{7k}{5}-\frac{5k}{5}=\frac{10}{2}\)
\(\Leftrightarrow7k-5k=10\)\(\Leftrightarrow2k=10\)\(\Leftrightarrow k=5\)( thoả mãn ĐK )
\(\Rightarrow a=5.4=20\)và \(b=5.7=35\)
Vậy số bé là 20 và số lớn là 35

Gọi x, y là 2 số đó.
Tổng của hai số bằng 23, ta có:
x + y = 23 (1)
2 lần số này lớn hơn số kia 1 đơn vị, ta có:
2x - y = 1 (2)
Từ (1), (2) có hệ phương trình: \(\left\{{}\begin{matrix}x+y=23\\2x-y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+2y=46\\2x-y=1\end{matrix}\right.\\ \Leftrightarrow3y=45\\ \Rightarrow y=15\Rightarrow x=\dfrac{1+15}{2}=8\)
Vậy 2 số đó là 15 và 8