L
2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
PT
1
TL
0
27 tháng 8 2021
a,
Gọi hai số tự nhiên liên tiếp là a và a + 1
Nếu a chia hết cho 2 thì bài toán được chứng minh.
Nếu a không chia hết cho 2 thì a = 2k + 1 (k∈N)
Suy ra: a + 1 = 2k + 1 + 1 = 2k + 2
Ta có: 2k ⋮ 2; 2 ⋮ 2
Suy ra: (2k + 2) ⋮ 2 hay (a + 1) ⋮ 2
Vậy trong hai số tự nhiên liên tiếp, có một số chia hết cho 2
Mik chỉ làm được câu a thôi nhưng vẫn mong bạn ủng hộ ^-^
TT
27 tháng 7 2017
a) hai số liên tiếp thì sẽ có 1 số chẵn và 1 số lẻ , số chẵn là số chia hết cho 2 nên trong hai số tự nhiên liên tiếp sẽ có 1 số chia hết cho 2
DB
3 tháng 8 2019
a) Vì có 1 số chẵn và 1 số lẻ trong 2 số tự nhiên liên tiếp nên chia hết cho 2
b) Trong 3 số tự nhiên liên tiếp thì có số cộng các chữ số của số đó chia hết cho3
c) Tổng 2 số tự nhiên liên tiếp là chẵn + lẻ = lẻ nên ko chia hết cho 2
d) 3 số tự nhiên liên tiếp thì có 1 số chia 3 dư 1 , 1 số chia 3 dư 2 , 1 số chia hết cho 3 nên lấy số dư là 1+2=3 chia hết cho 3 nên tổng 3 số tự nhiên liên tiếp chia hết cho 3
NH
1
21 tháng 11 2015
Số lớn nhất 100
Số bé nhất 1
Số các số hạng là: 100 - 1 + 1 = 100 (số)
Tổng là: 100 x (100 + 1):2 = 5050
Vậy chia hết cho 5
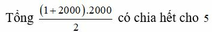
Số số hạng từ 1 đến 2000 là :
( 2000 - 1 ) : 1 + 1 = 2000 ( số )
Tổng dãy số liên tiếp từ 1 đến 2000 là :
( 2000 + 1 ) x 2000 : 2 = 2001000
Ví 2001000 có chữ số cuối cùng là 0 nên các số tự nhiên liên tiếp từ 1 đến 2000 chia hết cho 5
\(1+2+3+4+5+....+2000.\)
\(=\frac{1000-1+1}{2}.\left(2000+1\right)\)
\(=\frac{1000}{2}.2001\)
\(=500.2001\)
\(=1000500\)
Vì 1000500 tận cùng là 0 => tổng các số từ 1 đến 2000 chia hết cho 5.