Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A=(8+82)+(83+84)+...+(82013+82014)
=8(1+8)+83(1+8)+...+82013(1+8)
=9(8+83+85+...+82013)
=> A chia hết cho 9

A= 2015+20152+20153+....+20152013+20152014+20152015
A= ( 2015+20152 )+ ( 20153+20154 )+..... + (20152012+20152013) + (20152014+20152015)
A= 2015. (1+2015)+ 20153 .(1+2015) +.....+ 20152012. (1+2015)+ 20152014. (1+2015)
A= 2015.2016 + 20153.2016 +......+ 20152012.2016 + 20152014.2016
A= 2016. ( 2015+ 20153 +.......+20152012 + 20152014)
=> A chia hết cho 2016
=> đpcm : điều phải chứng minh

Bài 1 . Ta có 13^2014 là số lẻ
15^2015 là số lẻ => 13^2014+15^2015 là số chẵn chia hết cho 2
Bài 2 Ta có 121^2013 ko chia hết cho 5( có tận cùng là 1)
125^2014 chia hết cho 5( vì 125 chia hết cho 5)
=> 121^2013+125^2014 ko chia hết cho 5
Bài 1 . Ta có 13^2014 là số lẻ
15^2015 là số lẻ => 13^2014+15^2015 là số chẵn chia hết cho 2
Bài 2 Ta có 121^2013 ko chia hết cho 5﴾ có tận cùng là 1﴿
125^2014 chia hết cho 5﴾ vì 125 chia hết cho 5﴿ => 121^2013+125^2014 ko chia hết cho 5

a) Ta có: 22 + 23 + 24 + 25
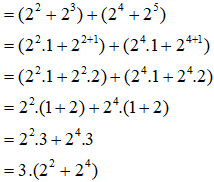
Vì 3 ⁝ 3 nên 3.(22 + 24) 3 hay (22 + 23 + 24 + 25) 3
Vậy tổng 22 + 23 + 24 + 25 chia hết cho 3
2 phút trước
a) Ta có: 22 + 23 + 24 + 25
Vì 3 ⁝ 3 nên 3.(22 + 24) 3 hay (22 + 23 + 24 + 25) 3
Vậy tổng 22 + 23 + 24 + 25 chia hết cho 3

a) ta có A= 2+2^2+2^3+2^4+2^5+2^6
=2*(1+2+2^2+2^3+2^4+2^5)
=2*63 =2*21*3 CHIA HẾT CHO 3( vì có một thứa số 3 trong tích )
còn lại bạn làm tương tự nha
2+22+23+.....+22013+22014
=(2+22)+(23+24)+...+(22013+22014)
=(2.1+2.2)+(23.1+23.2)+...+(22013.1+22013.2)
=2.(1+2)+23.(1+2)+...+22013.(1+2)
=2.3+23.3+..+22013.3
=3.(2+23+..+22013)
Vì 3 chia hết cho 3=> 2+22+23+...+22013+22014 chia hết cho 3