Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)
hay \(-x-4=3x+2\)
\(\Leftrightarrow-x-4-3x-2=0\)
\(\Leftrightarrow-4x-6=0\)
\(\Leftrightarrow-4x=6\)
hay \(x=-\dfrac{3}{2}\)
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được:
\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)
Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)
c) Vì (D2) song song với (D) nên a=-1
hay (D2): y=-x+b
Vì (D2) đi qua điểm B(-2;5)
nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được:
-(-2)+b=5
hay b=5-2=3
Vậy: (D2): y=-x+3
b) Vì A(xA;yA) là giao điểm của (D) và (D1) nên Hoành độ của A là nghiệm của phương trình hoành độ giao điểm có hai vế là hai hàm số của (D) và (D1)
hay \(-x-4=3x+2\)
\(\Leftrightarrow-x-4-3x-2=0\)
\(\Leftrightarrow-4x-6=0\)
\(\Leftrightarrow-4x=6\)
hay \(x=-\dfrac{3}{2}\)
Thay \(x=-\dfrac{3}{2}\) vào hàm số y=-x-4, ta được:
\(y=-\left(-\dfrac{3}{2}\right)-4=\dfrac{3}{2}-4=\dfrac{3}{2}-\dfrac{8}{2}=-\dfrac{5}{2}\)
Vậy: \(A\left(-\dfrac{3}{2};-\dfrac{5}{2}\right)\)
c) Vì (D2) song song với (D) nên a=-1
hay (D2): y=-x+b
Vì (D2) đi qua điểm B(-2;5)
nên Thay x=-2 và y=5 vào hàm số y=-x+b, ta được:
-(-2)+b=5
hay b=5-2=3
Vậy: (D2): y=-x+3

b: Vì (d)//y=3x+2 nên a=3
Vậy: (d): y=3x+b
Thay x=1 và y=2 vào (d), ta được:
b+3=2
hay b=-1
a: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}x^2+2x-3=0\\y=-2x+3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in\left\{-3;1\right\}\\y\in\left\{9;1\right\}\end{matrix}\right.\)

a:
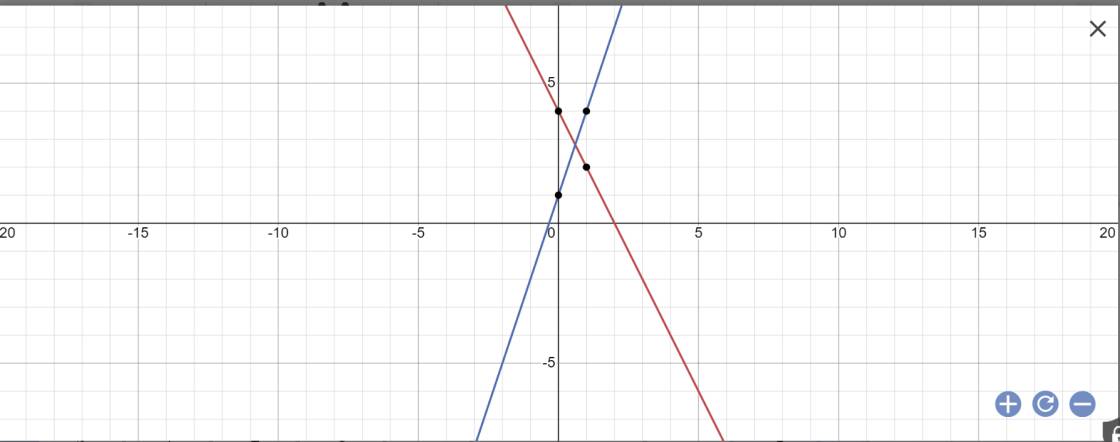
b: Phương trình hoành độ giao điểm là:
4-2x=3x+1
=>-2x-3x=1-4
=>-5x=-3
=>\(x=\dfrac{3}{5}\)
Thay x=3/5 vào y=3x+1, ta được:
\(y=3\cdot\dfrac{3}{5}+1=\dfrac{9}{5}+1=\dfrac{14}{5}\)
Vậy: \(N\left(\dfrac{3}{5};\dfrac{14}{5}\right)\)
c: (d'): y=3x+1
=>a=3
\(tan\alpha=a=3\)
=>\(\alpha\simeq71^034'\)

a: Thay x=2 và y=2 vào y=-x+4, ta được:
2=-2+4(đúng)
=>A thuộc (d)
b: Thay x=2 và y=2 vào y=ax^2, ta được:
a*4=2
=>a=1/2
=>y=1/2x^2
PTHĐGĐ là:
1/2x^2+x-4=0
=>x^2+2x-8=0
=>x=-4
=>y=1/2*(-4)^2=8

a:
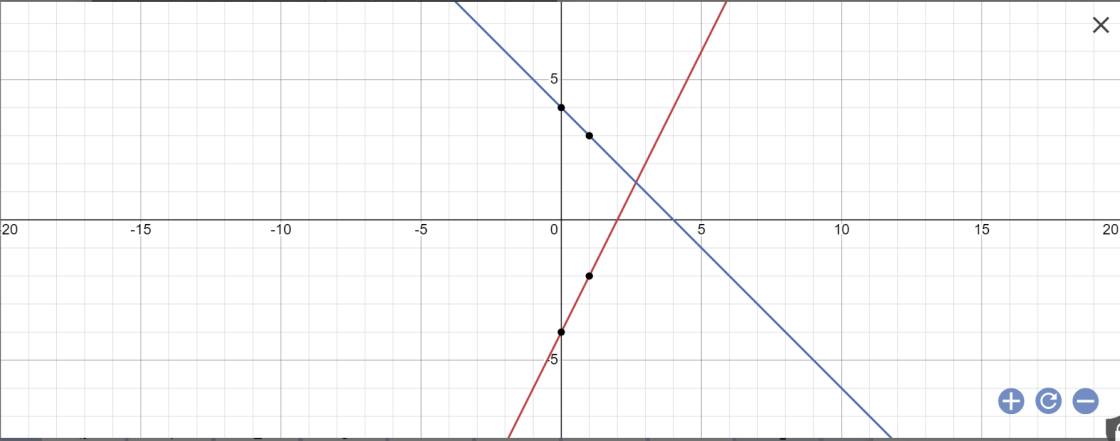
b: Tọa độ điểm Q là:
\(\left\{{}\begin{matrix}2x-4=-x+4\\y=-x+4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x=8\\y=-x+4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{8}{3}\\y=-\dfrac{8}{3}+4=\dfrac{4}{3}\end{matrix}\right.\)
Vậy: \(Q\left(\dfrac{8}{3};\dfrac{4}{3}\right)\)
Tọa độ M là:
\(\left\{{}\begin{matrix}x=0\\y=2x-4=2\cdot0-4=-4\end{matrix}\right.\)
Vậy: M(0;-4)
Tọa độ N là:
\(\left\{{}\begin{matrix}x=0\\y=-x+4=-0+4=4\end{matrix}\right.\)
vậy: N(0;4)
Q(8/3;4/3); M(0;-4); N(0;4)
\(QM=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(-4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{5}}{3}\)
\(QN=\sqrt{\left(0-\dfrac{8}{3}\right)^2+\left(4-\dfrac{4}{3}\right)^2}=\dfrac{8\sqrt{2}}{3}\)
\(MN=\sqrt{\left(0-0\right)^2+\left(4+4\right)^2}=8\)
Xét ΔMNQ có
\(cosMQN=\dfrac{QM^2+QN^2-MN^2}{2\cdot QM\cdot QN}=\dfrac{-1}{\sqrt{10}}\)
=>\(\widehat{MQN}\simeq108^026'\)
\(sinMQN=\sqrt{1-cos^2MQN}=\dfrac{3}{\sqrt{10}}\)
Diện tích tam giác MQN là:
\(S_{MQN}=\dfrac{1}{2}\cdot QM\cdot QN\cdot sinMQN\)
\(=\dfrac{1}{2}\cdot\dfrac{3}{\sqrt{10}}\cdot\dfrac{8\sqrt{5}}{3}\cdot\dfrac{8\sqrt{2}}{3}=\dfrac{32}{3}\)

a: PTHĐGĐ là:
x^2-3x+2=0
=>(x-2)(x-1)=0
=>x=2 hoặc x=1
Khi x=2 thì y=2^2=4
Khi x=1 thì y=1^2=1
b: Δ=(2m+2)^2-4(2m-3)
=4m^2+8m+4-8m+12
=4m^2+16>0
=>Phương trình luôn có hai nghiệm

Xét phương trình hoành độ giao điểm của 2 đường thẳng (d) và )d'):
- 3x - 2 = - x + 4.
<=> - 3x - 2 + x - 4 = 0.
<=> - 2x - 6 = 0.
<=> x = - 3.
=> y = 7.
Vậy tọa độ giao điểm của hai đường thẳng (d) và (d’) là (-3; 7).