Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



9) \(\left\{{}\begin{matrix}\dfrac{7}{2x+y}+\dfrac{4}{2x-y}=74\\\dfrac{3}{2x+y}+\dfrac{2}{2x-y}=32\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{21}{2x+y}+\dfrac{12}{2x-y}=222\\\dfrac{21}{2x+y}+\dfrac{14}{2x-y}=224\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{2x-y}=2\\\dfrac{7}{2x+y}+\dfrac{4}{2x-y}=74\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2x+y=\dfrac{1}{10}\\2x-y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-2y=\dfrac{9}{10}\\2x+y=\dfrac{1}{10}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{9}{20}\\x=\dfrac{11}{40}\end{matrix}\right.\)
10) \(\left\{{}\begin{matrix}x=2y-1\\2x-y=5\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2x-4y=-2\\2x-y=5\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=2y-1\\3y=7\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{11}{3}\\y=\dfrac{7}{3}\end{matrix}\right.\)
11) \(\left\{{}\begin{matrix}3x-6=0\\2y-x=4\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}3x=6\\y=\dfrac{x+4}{2}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3\end{matrix}\right.\)
12) \(\left\{{}\begin{matrix}2x+y=5\\x+7y=9\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}2x+y=5\\2x+14y=18\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x+y=5\\13y=13\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
13) \(\left\{{}\begin{matrix}\dfrac{3}{x}-\dfrac{4}{y}=2\\\dfrac{4}{x}-\dfrac{5}{y}=3\end{matrix}\right.\)(ĐKXĐ: \(x,y\ne0\))
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{12}{x}-\dfrac{16}{y}=8\\\dfrac{12}{x}-\dfrac{15}{y}=9\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{x}-\dfrac{4}{y}=2\\\dfrac{1}{y}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{2}\left(tm\right)\\y=1\left(tm\right)\end{matrix}\right.\)
14) \(\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{8}{x}+\dfrac{15}{y}=1\end{matrix}\right.\)(ĐKXĐ: \(x,y\ne0\))
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{8}{x}+\dfrac{8}{y}=\dfrac{2}{3}\\\dfrac{8}{x}+\dfrac{15}{y}=1\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{12}\\\dfrac{7}{y}=\dfrac{1}{3}\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}x=28\left(tm\right)\\y=21\left(tm\right)\end{matrix}\right.\)
15) \(\left\{{}\begin{matrix}2\sqrt{x-1}-\sqrt{y-1}=1\\\sqrt{x-1}+\sqrt{y-1}=2\end{matrix}\right.\)(ĐKXĐ: \(x\ge1,y\ge1\))
\(\Leftrightarrow\left\{{}\begin{matrix}3\sqrt{x-1}=3\\\sqrt{x-1}+\sqrt{y-1}=2\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{x-1}=1\\\sqrt{y-1}=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1=1\\y-1=1\end{matrix}\right.\)\(\Leftrightarrow x=y=2\left(tm\right)\)

1) Ta có: \(\left\{{}\begin{matrix}2\cdot\dfrac{x}{x+2}-\dfrac{y}{y-1}=4\\\dfrac{x}{x+2}-3\cdot\dfrac{y}{y-1}=-3\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2\cdot\dfrac{x}{x+2}-\dfrac{y}{y-1}=4\\2\cdot\dfrac{x}{x+2}-6\cdot\dfrac{y}{y-1}=-6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}-7\cdot\dfrac{y}{y-1}=10\\2\cdot\dfrac{x}{x+2}-\dfrac{y}{y-1}=4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{y}{y-1}=\dfrac{-10}{7}\\2\cdot\dfrac{x}{x+2}+\dfrac{10}{7}=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\cdot\dfrac{x}{x+2}=\dfrac{18}{7}\\\dfrac{y}{y-1}=\dfrac{-10}{7}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x}{x+2}=\dfrac{9}{7}\\\dfrac{y}{y-1}=\dfrac{-10}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9\left(x+2\right)=7x\\-10\left(y-1\right)=7y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}9x+18-7x=0\\-10y+10-7y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+18=0\\-17y+10=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x=-18\\-17y=-10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-9\\y=\dfrac{10}{17}\end{matrix}\right.\)
Vậy: Hệ phương trình có nghiệm duy nhất là \(\left(x,y\right)=\left(-9;\dfrac{10}{17}\right)\)

bạn vào link tham khảo
Câu hỏi của titanic - Toán lớp 7 - Học toán với OnlineMath

(d) : y = ax - 1
a, d vuông y = 2x + 3 <=> \(2a=-1\Leftrightarrow a=-\frac{1}{2}\)
b, d // y = - 5x + 7 <=> \(\hept{\begin{cases}a=-5\\-1\ne7\left(luondung\right)\end{cases}}\)
c, d \(\equiv\)y = 5x - 1 <=> \(a=5\)

\(x^2-4xy+5y^2=169\)
\(x^2-4xy+4y^2+y^2-169=0\)
\(\left(x^2-4xy+4y^2\right)+\left(y^2-13^2\right)=0\)
\(\left(x-2y\right)^2+\left(y-13\right)\left(y+13\right)=0\)
b/ \(\Leftrightarrow x^2-4xy+4y^2+y^2=13^2\)
\(\Leftrightarrow\left(x-2y\right)^2=\left(13^2-y^2\right)\)
\(\Rightarrow y^2\le13^2\)và \(13^2-y^2\)là số chính phương . Do đó :
\(y^2=0\)hay \(y=0\)
Thay vào ta có các nghiệm sau \(\left(13,0\right);\left(-13;0\right)\)

a, Ta có : d // d' <=> \(a=\frac{1}{2}\)
Vì đồ thị hàm đi qua A( 2 ; - 2 ) nên thay x = 2 ; y = -2 vào (d)
phương trình đường thẳng (d) có dạng : \(2a+b=-2\)
\(\Rightarrow b=-2\)
Vậy a = 1/2 ; b = -2
d, (d) cắt Ox tại B( 1/2 ; 0 ) => OB = 1/2
(d) cắt Oy tại C ( 0 ; -2 ) => OC = 2
tam giác OBC vuông tại O
\(\Rightarrow S_{OBC}=\frac{1}{2}.OB.OC=\frac{1}{2}\left(đvdt\right)\)
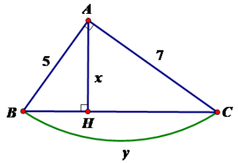
Đáp án A
Theo định lý Pytago ta có:
B C 2 = A B 2 + A C 2 ⇔ B C 2 = 74
⇔ BC = 74
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông ta có: