Tính và so sánh: 10 5 2...

Khách

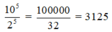
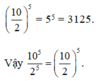
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

28 tháng 4 2017

Tính và so sánh: 10 5 2 5 v à 10 2 5

#Hỏi cộng đồng OLM #Toán lớp 7

Cao Minh Tâm

28 tháng 4 2017

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

Luyện Hoàng Khánh Linh

11 tháng 11 2016 - olm

Câu 1: Chứng minh:

\(31.82+125.48+21.43=125.67=1500\)

Câu 2: So sánh:

1,\(\sqrt{51}-\sqrt{5}v\text{à}\sqrt{20}-\sqrt{6}\)

2,\(\sqrt{2}+\sqrt{8}v\text{à}\sqrt{3}+3\)

3,\(\sqrt{37}-\sqrt{14}v\text{à}6-\sqrt{15}\)

4,\(\sqrt{5}+\sqrt{10}v\text{à}5,3\)

#Hỏi cộng đồng OLM #Toán lớp 7

bùi thị kim trang

4 tháng 7 2016 - olm

tính và so sánh. giúp mình nha

\(\left(\frac{_{-2}}{3}\right)^3\)và \(\frac{\left(-2\right)^3}{3^3}\)

\(\frac{10^5}{2^5}\)và \(\left(\frac{10}{2}\right)^5\)

#Hỏi cộng đồng OLM #Toán lớp 7

o0o I am a studious person o0o

4 tháng 7 2016

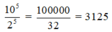
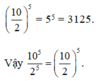
\(\left(\frac{-2}{3}\right)^3=\frac{-8}{27}\)

\(\frac{\left(-2\right)^3}{3^3}=\frac{-8}{27}\)

\(=>\left(-\frac{2}{3}\right)^3=\frac{\left(-2\right)^3}{3^3}\)

Áp dụng câu trên ta được :

\(\frac{10^5}{2^5}=\left(\frac{10}{2}\right)^5\)

Ủng hộ nha

Đúng(0)

Trà My

4 tháng 7 2016

o0o I am a studious person o0o:cái này có công thức trong sách giáo khoa rồi cần j phải tính

Đúng(0)

Nguyen Ngoc Lien

13 tháng 9 2016

Tính và so sánh :

a) \(\left(\frac{-2}{3}\right)^3\) và \(\frac{\left(-2\right)^3}{3^3}\)

b) \(\frac{10^5}{2^5}\)và \(\left(\frac{10}{2}\right)^5\)

#Hỏi cộng đồng OLM #Toán lớp 7

Phan Cả Phát

13 tháng 9 2016

\(\left(-\frac{2}{3}\right)^3=\frac{\left(-2\right)^3}{3^3}\)

mà \(\frac{\left(-2\right)^3}{3^3}\) là vế phải

\(\Rightarrow\) \(\left(-\frac{2}{3}\right)^3=\frac{\left(-2\right)^3}{3^3}\)

\(\frac{10^5}{2^5}=\left(\frac{10}{2}\right)^5\)

mà \(\left(\frac{10}{2}\right)^5\) là vế phải

Nên \(\frac{10^5}{2^5}=\left(\frac{10}{2}\right)^5\)

Đúng(0)

soyeon_Tiểubàng giải

13 tháng 9 2016

a) \(\left(-\frac{2}{3}\right)^3=\left(-\frac{2}{3}\right).\left(-\frac{2}{3}\right).\left(-\frac{2}{3}\right)=\frac{\left(-2\right).\left(-2\right).\left(-2\right)}{3.3.3}=\frac{\left(-2\right)^3}{3^3}=\frac{-8}{27}\)

b) \(\left(\frac{10}{2}\right)^5=\frac{10}{2}.\frac{10}{2}.\frac{10}{2}.\frac{10}{2}.\frac{10}{2}=\frac{10.10.10.10.10}{2.2.2.2.2}=\frac{10^5}{2^5}=\frac{100000}{32}=3125\)

Đúng(0)

Nguyễn Thị Thùy Dương

11 tháng 11 2017 - olm

a) so sánh 4\(\frac{8}{3}\) và 3\(\sqrt{2}\)

b)so sánh 5 \(\sqrt{\left(-10\right)^2}\)và 10 \(\sqrt{\left(-5\right)^2}\)

#Hỏi cộng đồng OLM #Toán lớp 7

Quách Quách Cá Tính

11 tháng 11 2017

kết bạn với nhau được không dương

Đúng(0)

Nguyễn Thị MInh Huyề

27 tháng 6 2019 - olm

So sánh

\(a,2^{30}+3^{30}+4^{30}v\text{à}3^{20}+6^{20}+8^{20}\)

\(b,2^{30}+3^{30}+4^{30}v\text{à}3.24^{10}\)

\(c,2^0+2^1+2^2+...+2^{50}v\text{à}2^{51}\)

#Hỏi cộng đồng OLM #Toán lớp 7

Kiệt Nguyễn

28 tháng 6 2019

c) Đặt \(A=2^0+2^1+2^2+...+2^{50}\)

\(\Leftrightarrow2A=2^1+2^2+2^3...+2^{51}\)

\(\Leftrightarrow2A-A=2^1+2^2+2^3...+2^{51}\)\(-2^0-2^1-2^2-...-2^{50}\)

\(\Leftrightarrow A=2^{51}-2^0=2^{51}-1< 2^{51}\)

Vậy \(2^0+2^1+2^2+...+2^{50}< 2^{51}\)

Đúng(1)

Kiệt Nguyễn

28 tháng 6 2019

a)Ta có: \(\hept{\begin{cases}2^{30}=\left(2^3\right)^{10}=8^{10}\\3^{30}=\left(3^3\right)^{10}=27^{10}\\4^{30}=\left(2^2\right)^{30}=2^{60}\end{cases}}\)và \(\hept{\begin{cases}3^{20}=\left(3^2\right)^{10}=9^{10}\\6^{20}=\left(6^2\right)^{10}=36^{10}\\8^{20}=\left(2^3\right)^{20}=2^{60}\end{cases}}\)

Mà \(8^{10}< 9^{10}\); \(27^{10}< 36^{10}\);\(2^{60}=2^{60}\)nên

\(8^{10}+27^{10}+2^{60}< 9^{10}+36^{10}+2^{60}\)

hay \(2^{30}+3^{30}+4^{30}< 3^{20}+6^{20}+8^{20}\)

Đúng(0)