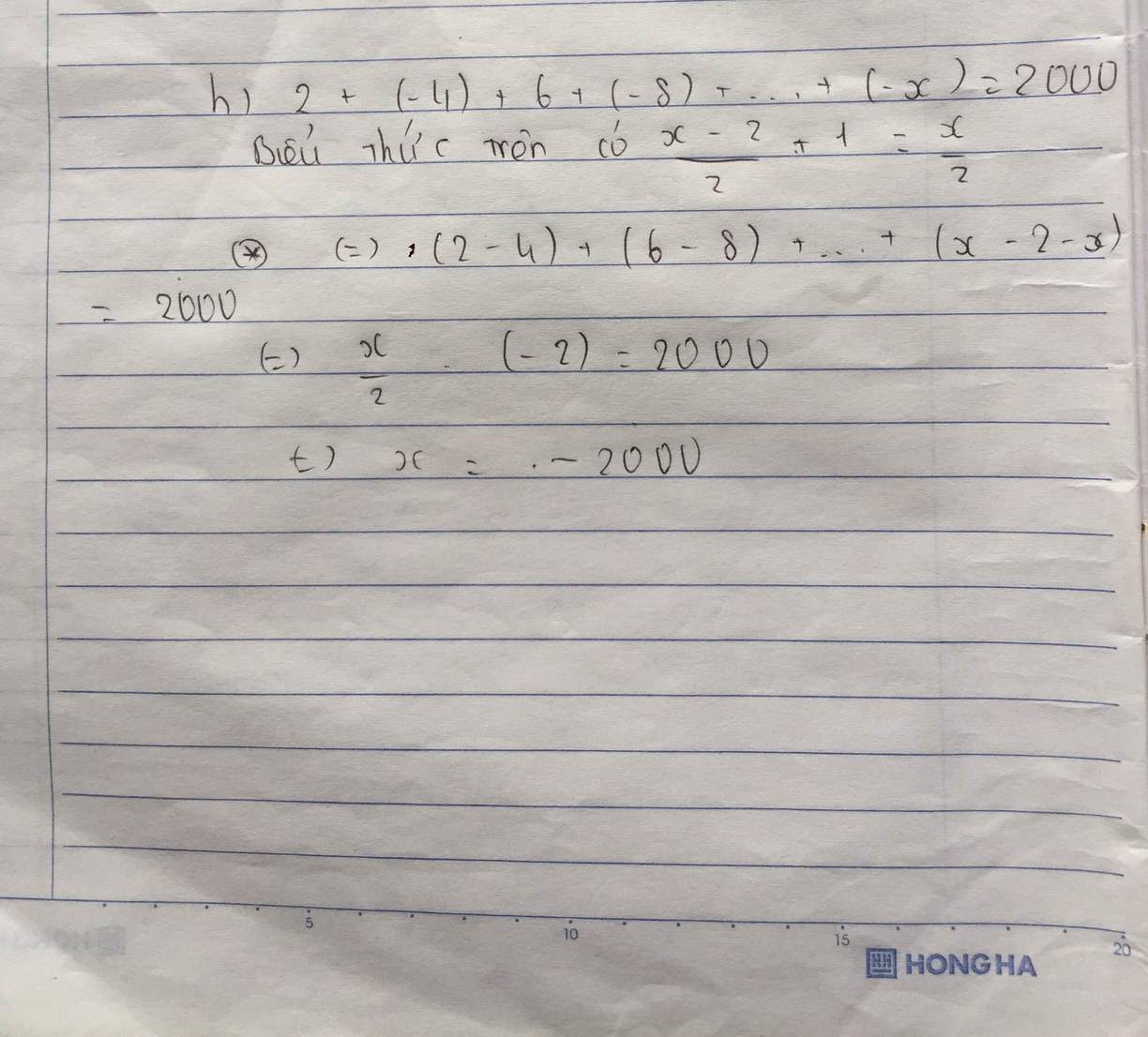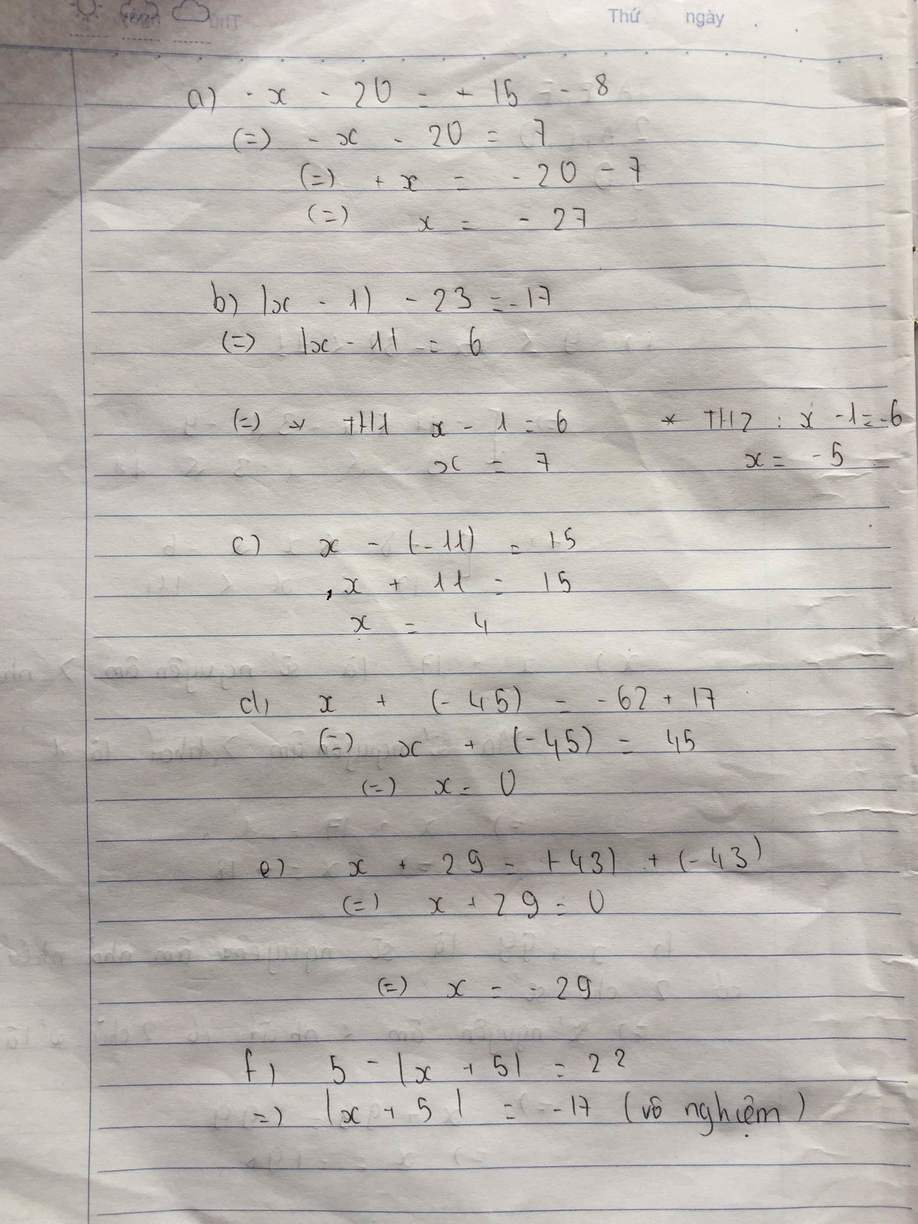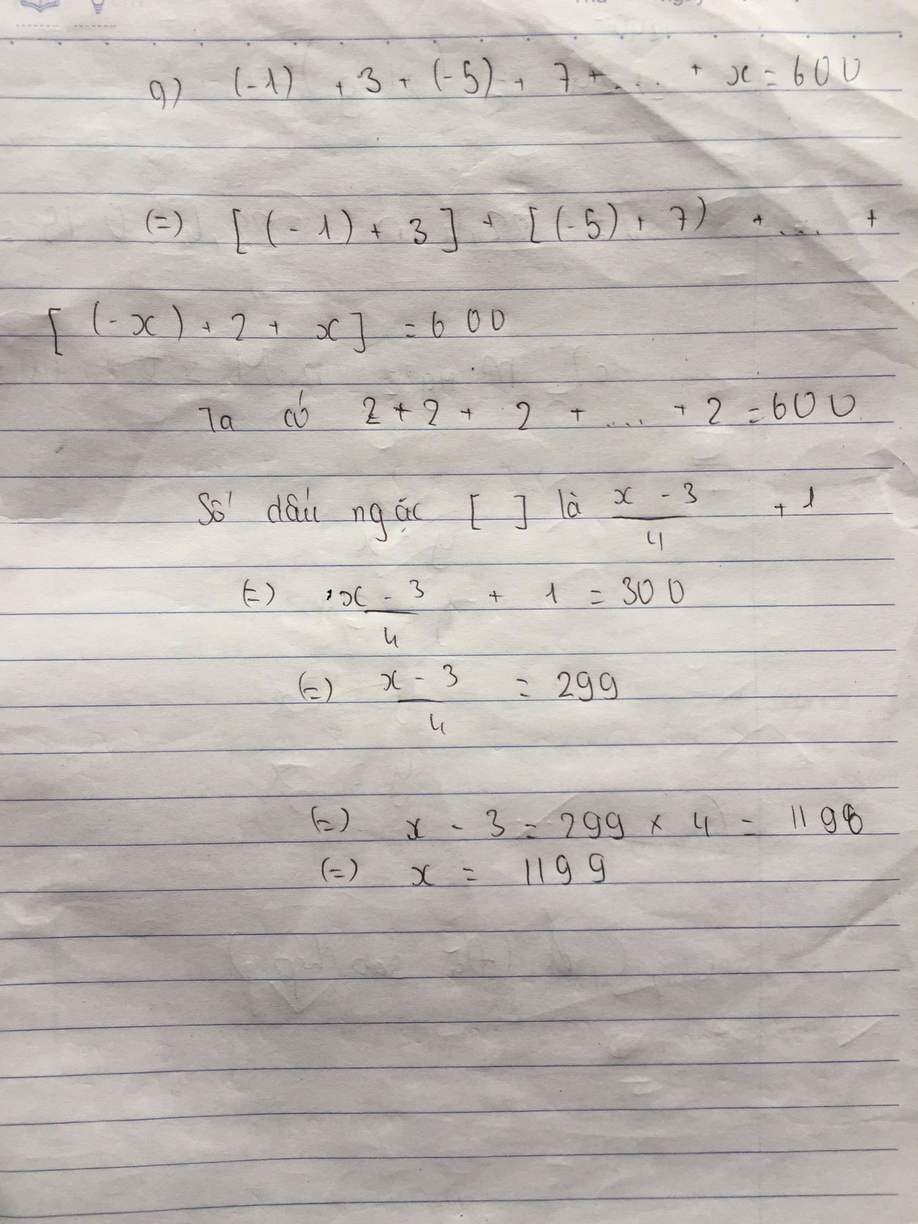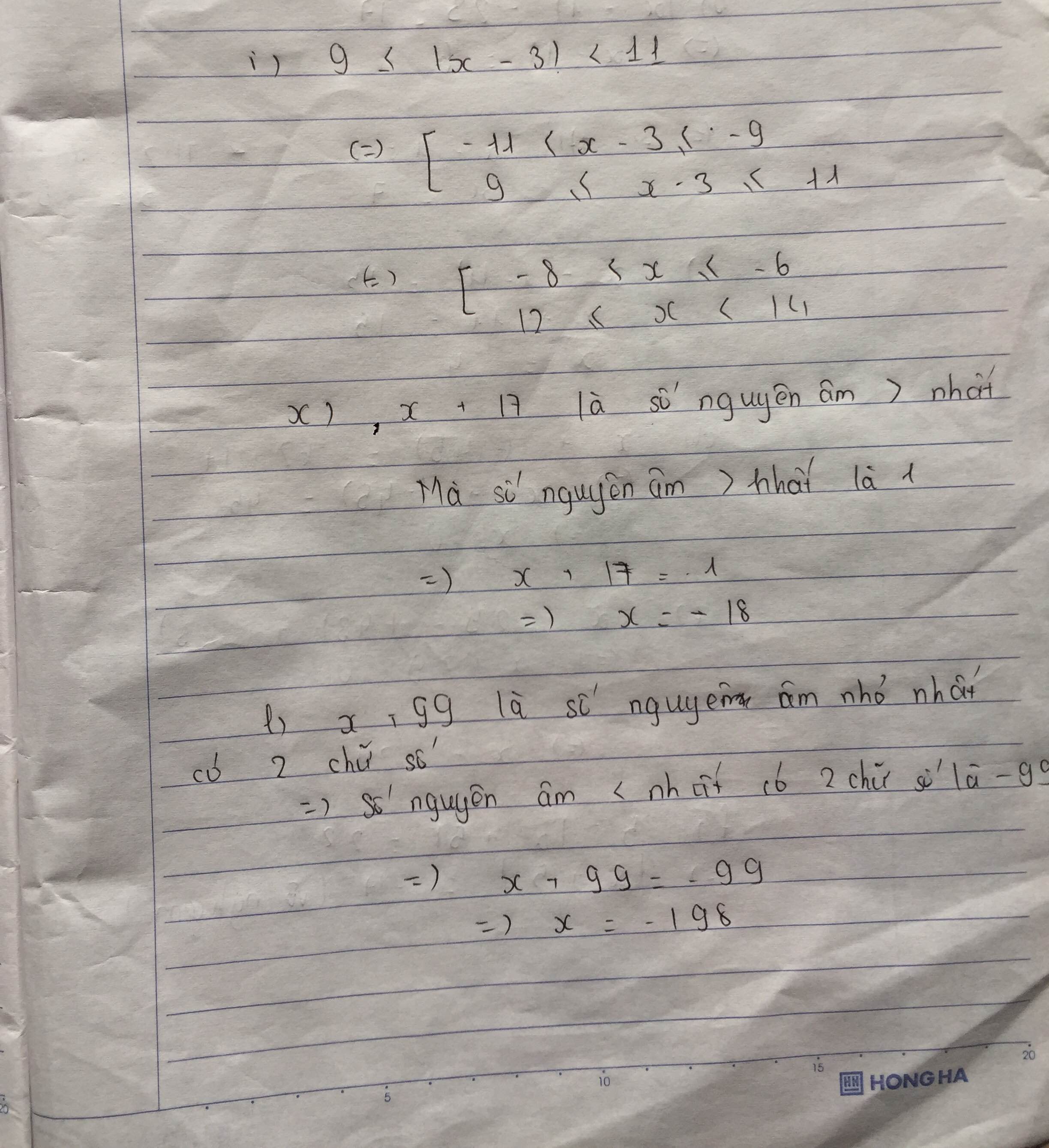Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(a.-7< x< -1\\ x\in\left\{-6;-5;-4;-3;-2\right\}\\ \Rightarrow\left(-6\right)+\left(-5\right)+\left(-4\right)+\left(-3\right)+\left(-2\right)\\ =-20\)
\(b.-1\le x\le6\\ x\in\left\{-1;0;1;2;3;4;5;6\right\}\\ \Rightarrow\left(-1\right)+0+1+2+3+4+5+6\\ =20\)
\(c.-5\le x< 6\\ x\in\left\{-5;-4;-3;-2;-1;0;1;2;3;4;5\right\}\\ \Rightarrow-5-4+-3+-2+-1+0+1+2+3+4+5\\ =0\)

a/ 5-x=-17
x= 5-(-17)
x= 5+17
x= 22
b/ |x-1| - 17 = 3
|x-1| = 3+17
|x-1| =20
=> x-1 = 20 hoặc x-1 = -20
=> x =20+1 hoặc x = -20 +1
=> x= 21 hoặc x= -19

a: \(A=\left|x+1\right|+\left|y-2\right|\ge0\forall x,y\)
Dấu '=' xảy ra khi x=-1 và y=2
b: \(B=\left|x-4\right|+\left|y+6\right|\ge0\forall x,y\)
Dấu '=' xảy ra khi x=4 và y=-6

ta có \(\left|x+1\right|+\left|y-2\right|\ge0\)
\(\Leftrightarrow\left|x+1\right|+\left|y-2\right|=0\)
\(\Leftrightarrow\hept{\begin{cases}x+1=0\\y-2=0\end{cases}\Rightarrow\hept{\begin{cases}x=-1\\y=2\end{cases}}}\)
câu b tương tự
A ,B đều là tổng của hai số không âm=> nhỏ nhất KHi các số hạng của nó bằng 0
a)x+1=0; y-2=0
x=-1 và y=2
b)x=4 và y=-6

/x-3/=4+16
/x-3/=20
th1 (x-3)=20 th2 (x-3) = -20
x=20+3 x=-20+3
x=23 x=-17
a) I x-3 I - 16 = 4 th1 x-3 = 20 th2 x-3= -20
I x-3 I = 4+16 x = 20 -3 x = -20 - 3
I x-3I = 20 x = 17 x = -23
suy ra x-3= 20 hoặc x-3 =-20 Vậy x=17 hoặc x= -23
b) 26 - I x+9I = -13 th1 x + 9=39 th2 x+ 9=(-39)
I x+9I = 26-(-13) x=39-9 x=-39 -9
I x+9I=39 x=30 x=-48
suy ra x+9=39 hoặc x+9=(-39) Vậy x=30 hoặc x= -48

Câu 2:
a: Để A là số nguyên thì \(x-1\in\left\{1;-1;3;-3\right\}\)
hay \(x\in\left\{2;0;4;-2\right\}\)
b: Để -4/2x-1 là số nguyên thì \(2x-1\in\left\{1;-1;2;-2;4;-4\right\}\)
hay \(x\in\left\{1;0;\dfrac{3}{2};-\dfrac{1}{2};\dfrac{5}{2};-\dfrac{3}{2}\right\}\)
c: Để 3x+7/x-1là số nguyên thì \(3x-3+10⋮x-1\)
\(\Leftrightarrow x-1\in\left\{1;-1;2;-2;5;-5;10;-10\right\}\)
hay \(x\in\left\{2;0;3;-1;6;-4;11;-9\right\}\)
d: Để 4x-1/x-3 là số nguyên thì \(4x-12+11⋮x-3\)
\(\Leftrightarrow x-3\in\left\{1;-1;11;-11\right\}\)
hay \(x\in\left\{4;2;14;-8\right\}\)