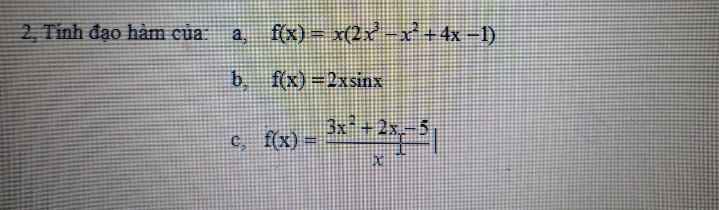Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

j, ĐK: \(x\ne\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
\(tan\left(\dfrac{\pi}{3}+x\right)-tan\left(\dfrac{\pi}{6}+2x\right)=0\)
\(\Leftrightarrow tan\left(\dfrac{\pi}{3}+x\right)=tan\left(\dfrac{\pi}{6}+2x\right)\)
\(\Leftrightarrow\dfrac{\pi}{3}+x=\dfrac{\pi}{6}+2x+k\pi\)
\(\Leftrightarrow x=\dfrac{\pi}{6}+k\pi\left(l\right)\)
\(\Rightarrow\) vô nghiệm.

ta có
\(lim\frac{\sqrt{n+4}}{\sqrt{n}+1}=lim\frac{\sqrt{n+4}:\sqrt{n}}{\left(\sqrt{n}+1\right):\sqrt{n}}=lim\frac{\sqrt{1+\frac{4}{n}}}{1+\frac{1}{\sqrt{n}}}=1\)

Lập số có 5 chữ số bất kì (các chữ số khác nhau): \(5!-4!\) số
Xếp 1 và 2 cạnh nhau: \(2!=2\) cách
Coi cặp 12 như một số, hoàn vị với 3 chữ số còn lại (sẽ tạo thành số có 5 chữ số sao cho 1 và 2 cạnh nhau): \(4!-3!\) số
\(\Rightarrow\) Có \(2.\left(4!-3!\right)\) số mà 1 và 2 cạnh nhau
\(\Rightarrow\) Số số để 1 và 2 không liền nhau:
\(5!-4!-2.\left(4!-3!\right)=60\) số

Lời giải:
Gọi số thỏa mãn điều kiện đề bài là $\overline{a_1a_2a_3a_4a_5}$
$a_1$ có 9 cách chọn $(1,2,...,9)$
$a_2,a_3,a_4$ có 10 cách chọn $(0,1,2,...,9)$
Nếu $a_1+a_2+a_3+a_4$ chẵn thì $a_5$ có 5 cách chọn để tổng cả 5 số là chẵn
Nếu $a_1+a_2+a_3+a_4$ lẻ thì $a_5$ cũng có 5 cách chọn để tổng cả 5 số là số chẵn
Như vậy, đối với mỗi giá trị $a_1,a_2,a_3,a_4$ thì ta có $5$ cách chọn $a_5$ để $a_1+a_2+a_3+a_4+a_5$ chẵn
Do đó, có $9.10^3.5=45000$ số thỏa mãn đề.

a.
Do chóp tứ giác đều \(\Rightarrow\Delta SAC\) cân tại A
Mà O là tâm đáy \(\Rightarrow O\) là trung điểm AC
\(\Rightarrow SO\perp AC\) (trung tuyến đồng thời là đường cao trong tam giác cân)
Hoàn toàn tương tự, ta có \(SO\perp BD\)
\(\Rightarrow SO\perp\left(ABCD\right)\)
b.
Ta có: \(AC\perp BD\) (hai đường chéo hình vuông)
Theo cmt, \(SO\perp AC\)
\(\left\{{}\begin{matrix}SO\in\left(SBD\right)\\BD\in\left(SBD\right)\end{matrix}\right.\) \(\Rightarrow AC\perp\left(SBD\right)\)
Tương tự: \(\left\{{}\begin{matrix}BD\perp AC\\BD\perp SO\left(cmt\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)

a, \(f\left(x\right)=2x^4-x^3+4x^2-x\)
\(\Rightarrow f'\left(x\right)=\left(2x^4-x^3+4x^2-x\right)'\)
\(=\left(2x^4\right)'-\left(x^3\right)'+\left(4x^2\right)'-\left(x\right)'\)
\(=2.4x^3-3x^2+4.2x-1\)
\(=8x^3-3x^2+8x-1\)
b, \(f\left(x\right)=2sinx\)
\(\Rightarrow f'\left(x\right)=\left(2sinx\right)'=2cosx\)
c, \(f\left(x\right)=\dfrac{3x^2+2x-5}{x}\)
\(\Rightarrow f'\left(x\right)=\left(\dfrac{3x^2+2x-5}{x}\right)'\)
\(=\left(3x+2-\dfrac{5}{x}\right)'\)
\(=\left(3x\right)'+\left(2\right)'-\left(\dfrac{5}{x}\right)'\)
\(=3+0+\dfrac{5}{x^2}=\dfrac{5}{x^2}+3\)