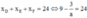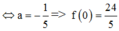Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đáp án C
Phương pháp :
+) Viết phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ m – 2
y = f’(m – 2)(x – m +2)+y(m – 2) (d)
+) Xác định các giao điểm của d và các đường tiệm cận => x2;y1
+) Thay vào phương trình x2 + y1 = –5 giải tìm các giá trị của m.
Cách giải: TXĐ: D = R\ {–2}
Ta có 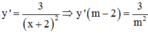
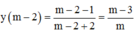
=>Phương trình tiếp tuyến của đồ thị hàm số tại điểm có hoành độ m – 2 là: 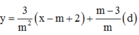
Đồ thị hàm số y = x - 1 x + 2 có đường TCN y = 1và tiệm cậm đứng x = –2
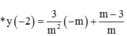
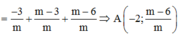
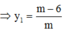
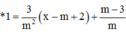
![]()
![]()
![]()
![]()
![]()
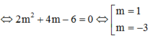
![]()

Đáp án D
Dựa vào đồ thị hàm số y = f ' ( x ) ⇒ f ' x = 3 x 2 - 1
Khi đó f x = ∫ f ' x d x = x 3 - 3 x + C .
Điều kiện đồ thị hàm số f(x) tiếp xúc với đường thẳng y = 4 là:
f x = 4 f x = 0 ⇒ x 3 - 3 x + C = 4 3 x 2 - 1 = 0 ⇔ x = - 1 C = 2 (Do x < 0 suy ra f x = x 3 - 3 x + 2 C
Cho C ∩ O x ⇒ hoành độ các giao điểm là x = -2,x = 1
Khi đó S = ∫ - 2 1 x 3 - 3 x + 2 d x = 27 4 .

Đáp án A
Phương trình hoành độ giao điểm:
x 2 + x + 3 x − 2 = x x ≠ 2 ⇒ x 2 + x + 3 = x 2 − 2 x ⇔ x = − 1 t / m .

Đáp án C
Giả sử ![]()
Hoành độ điểm D là nghiệm phương trình: ![]()
![]()
![]()
![]()
Hoành độ điểm E là nghiệm của phương trình: ![]()
![]()
![]()
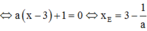
Hoành độ điểm F là nghiệm của phương trình: ![]()
![]()
![]()
![]()
Khi đó