Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt \(t=\sqrt{1-x}\)
\(\Rightarrow\begin{cases}x=1-t^2\\dx=-2tdt\end{cases}\) \(\Leftrightarrow\frac{x^2dx}{\sqrt{1-x}}\)\(=\frac{\left(1-t^2\right)\left(-2tdt\right)}{t}=-2\left(1-2t^2+3t^4-t^6\right)dt\)
Vậy : \(\int\frac{x^3dx}{\sqrt{1-x}}=\int\left(-2+4t^2-6t^4+2t^6\right)dt=-2t+\frac{4}{3}t^3-\frac{6}{5}t^5+\frac{2}{7}t^7+C\)
= \(-2\sqrt{1-x}+\frac{4}{3}\left(1-x\right)\sqrt{1-x}-\frac{6}{5}\left(1-x\right)^2\sqrt{1-x}+\frac{2}{7}\left(1-x\right)^3\sqrt{1-x}+C\)

Đặt \(t=2-3x^2\)\(\Rightarrow\begin{cases}dt=-6xdx\\x^2=\frac{2-t}{3}\end{cases}\)\(\Leftrightarrow x^2\left(2-3x^2\right)^8=\left(\frac{2-t}{3}\right)t^8=\frac{1}{3}\left(2t^8-t^9\right)\)
Vậy :
\(I=\int x^2\left(2-3x^2\right)^8dx=\frac{1}{3}\left(2\int t^8dt-\int t^9dt\right)=\frac{2}{27}t^9-\frac{1}{30}t^{10}+C\)
\(=\frac{2}{27}\left(2-3x^2\right)^9-\frac{1}{30}\left(2-3x^2\right)^{10}+C\)

Đáp án C
Phương pháp:
Đặt ẩn phụ t = ln x.
Cách giải:
Ta có:
![]()
![]()
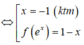
Đặt
![]()
Khi đó :
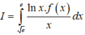
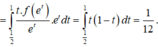

a1sinx+b1cosx=A(a2sinx+b2cosx)+B(a2cosx-b2sinx) roi the vo ,do la dung dong nhat thuc

Đáp án D
Phương pháp:
Sử dụng công thức từng phần.
Cách giải:
Ta có :
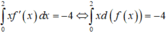
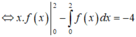
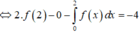
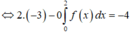
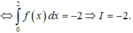

Ta thực hiện theo các bước sau :
Bước 1 : Biến đổi
\(a_1\sin x+b_1\cos x+c_1=A\left(a_2\sin x+b_2\cos x+c_2\right)+B\left(a_2\cos x+b_2\sin x\right)+C\)
Bước 2 : Khi đó :
\(I=\int\frac{A\left(a_2\sin x+b_2\cos x+c_2\right)+B\left(a_2\cos x+b_2\sin x\right)+C}{_2\sin x+b_2\cos x+c_2}\)
\(=A\int dx+B\int\frac{\left(a_2\cos_{ }x-b_2\sin x_{ }\right)dx}{_{ }a_2\sin x+b_2\cos x+c_2}+C\int\frac{dx}{a_2\sin x+b_2\cos x+c_2}\)
\(=Ax+B\ln\left|a_2\sin x+b_2\cos x+c_2\right|+C\int\frac{dx}{a_2\sin x+b_2\cos x+c_2}\)
Trong đó :
\(\int\frac{dx}{a_2\sin x+b_2\cos x+c_2}\)

- Loại 1: Đặt t=u(x)
- Loại 2: Đặt x=u(t)
Phương pháp đổi biến loại 1
Bài toán: Tính tích phân dạng: I=∫abf(u(x))(u(x))′dx
Phương pháp:
Đặt t=u(x)⇒dt=u′(x)dx
Đổi cận:
![]()
⇒I=∫u(a)u(b)f(t)dt
Ví dụ 1: Tính các tích phân sau:
a) I=∫01ex2+1xdx
Phân tích: Ta thấy có thể viết lại: I=∫01ex2+1xdx=∫01ex2+112.2xdx=12∫01ex2+1.2xdx
Trong đó 2x là đạo hàm của x2+1 nên ta có thể đặt t=x2+1.
Giải
Đặt t=x2+1⇒dt=2xdx
Đổi cận:
![]()
⇒I=12∫12etdt=12et∣∣∣21=12(e2−e)
b) J=∫01x3x2+1−−−−−√dx
Đặt t=x2+1−−−−−√⇒t2=x2+1⇒x2=t2−1⇒xdx=tdt
Đổi cận:
![]()
⇒J=∫01x2.x2+1−−−−−√.xdx=∫12√(t2−1).t.tdt=∫12√(t4−t2)dt
=(t55−t33)∣∣∣2–√1=22√+215
Một số bài tập áp dụng
1) J1 = ∫12xex2dx 2) J2 = ∫1e1+lnx√xdx
3) J3 = ∫01x3(x4−1)5dx 4) J4 = ∫024−x2−−−−−√.xdx
5) J5 = ∫0π/2cosx(1+sinx)4dx
Phương pháp đổi biến loại 2
Trong một số trường hợp đặt biệt, ta sẽ đổi biến bằng cách đặt x=u(t) để chuyển từ biến x về biến t. Một số trường hợp mà ta thường gặp có thể áp dụng phương pháp này:
1) Hàm số có chứa a2−x2−−−−−−√: đặt x=|a|sint với (−π2≤t≤π2) hoặc x=|a|cost với (0≤t≤π).
2) Hàm số có chứa x2−a2−−−−−−√: đặt x=|a|sint với (−π2≤t≤π2;t≠0) hoặc x=|a|cost với (0≤t≤π;t≠π2).
3) Hàm số có chứa a2+x2: đặt x=|a|tant với (−π2≤t≤π2) hoặc x=|a|cott với (0≤t≤π).
Ví dụ 3: Tình các tích phân sau:
a) I=∫024−x2−−−−−√dx
Giải
Đặt x=2sint (−π2≤t≤π2)
⇒dx=2costdt
Đổi cận:

⇒I=∫0π24−4sin2t−−−−−−−−√.2costdt=∫0π24(1−sin2t)−−−−−−−−−−√.2costdt
=∫0π24cos2t−−−−−√.2costdt=∫0π24cos2tdt=∫0π22(1+cos2t)dt
=2(t+12sin2t)∣∣∣π20=π
b) J=∫01x1+x2dx
Giải
Đặt x=tant⇒dx=1cos2tdt (−π2≤t≤π2)
Đổi cận:

⇒J=∫0π4tant1+tan2t(1+tan2t)dt=∫0π4tantdt=∫0π4sintcostdt
=−∫0π4(cost)′costdt=−ln(cost)∣∣∣π40=−ln2√2
Một số bài tập áp dụng:
1) ∫01dx1+x2 2) ∫02√2−x2−−−−−√dx 3) ∫2√2dxxx2−1√
4) ∫123√2dx1−x2√ 5) ∫13√9+3x2√dxx2
Định nghĩa : Cho f(x) là một hàm số liên tục trên đoạn [a; b] và giả sử F(x) là một nguyên hàm của f(x) trên đoạn [a; b]. Khi đó hiệu F(b)−F(a) được gọi là tích phân từ a đến b của hàm số f(x).
Các phương pháp giải tích phân :
PHƯƠNG PHÁP TÍCH PHÂN TỪNG PHẦN

Cách đặt: Nhất lốc, nhì đa, tam lượng, tứ mũ (hàm logarit, hàm đa thức, hàm lượng giác, hàm mũ)

Đáp án B


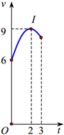
Từ đồ thị ta thấy ∫ - 5 3 g x d x là số dương. Mà 4 đáp án chỉ có B là phù hợp, nên ta chọn B.
Chú ý: Có thể tính ∫ - 5 3 g x d x như sau
Từ đồ thị hàm số y = g x ta thấy nó đi qua các điểm - 5 ; 2 , - 2 ; 0 , 0 ; 0 nên ta có:
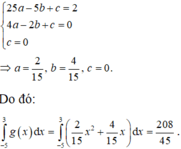
Giả sử vận tốc của vật chuyển động có phương trình là:

![]()