Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn nên viết đề bằng công thức toán để mọi người hiểu đề hơn


\(I=\int\limits^{\dfrac{\pi}{4}}_0xsinxdx\)
Đặt \(\left\{{}\begin{matrix}u=x\\dv=sinxdx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=-cosx\end{matrix}\right.\)
\(\Rightarrow I=-x.cosx|^{\dfrac{\pi}{4}}_0+\int\limits^{\dfrac{\pi}{4}}_0cosxdx=\left(-x.cosx+sinx\right)|^{\dfrac{\pi}{4}}_0=-\dfrac{\pi\sqrt{2}}{8}+\dfrac{\sqrt{2}}{2}\)

\(\int_1^2\sqrt{1+x}dx=\int_1^2\sqrt{1+x}d(1+x)=\dfrac{2}{3}(1+x)^{3/2}|_1^2=...\)


= 1 / e . ( t/p từ 1->e ( e.lnx / ( x + 1 ) ) dx
= 1 / e . ( tp từ 1->e ( ln(x+1) / ( x + 1 ) ) dx < e.lnx = ln ( x + 1 ) mà >
= 1 / e . ( tp từ 1->e ( ln(x+1) d ( ln ( x + 1 ) )
= 1 / e . ( 1 /2 . ln^2 (( x + 1 )) |1->e )
= ( ln^2 (( e + 1 )) - ln2 ) / 2e
\(I=\int_1^e\dfrac{\ln x}{x}dx=\int_1^e\ln x.d(\ln x)=\dfrac{(\ln x)^2}{2}|_1^e=...\)

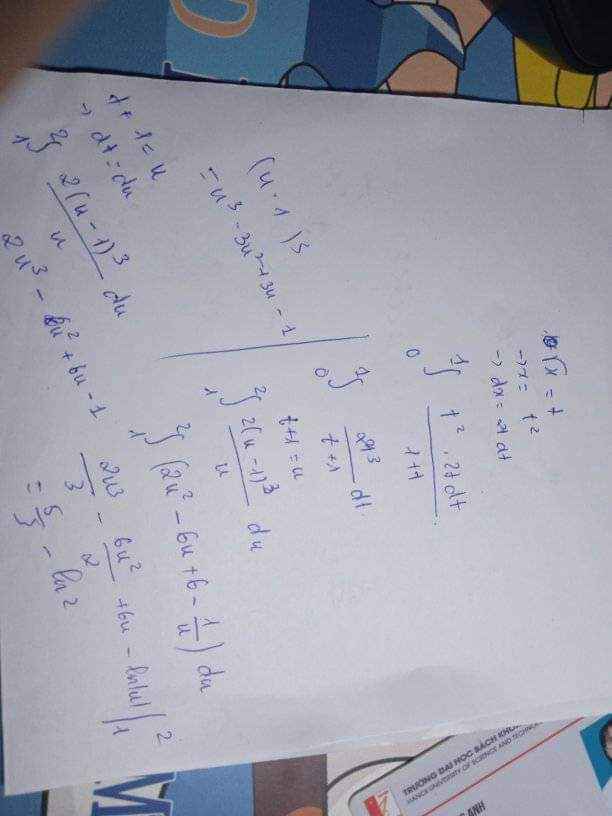
\(I_1=\int\limits^0_{-1}x\left(x^2-4\right)^{2019}dx=\dfrac{1}{2}\int\limits^0_{-1}\left(x^2-4\right)^{2019}d\left(x^2-4\right)\)
\(=\dfrac{1}{4040}\left(x^2-4\right)^{2020}|^0_{-1}=\dfrac{4^{2020}-3^{2020}}{4040}\)
\(I_2=\int\limits^0_{-1}x\left(x-6\right)^{2019}dx\)
Đặt \(x-6=t\Rightarrow dx=dt;\left\{{}\begin{matrix}x=-1\Rightarrow t=-7\\x=0\Rightarrow t=-6\end{matrix}\right.\)
\(\Rightarrow I_2=\int\limits^{-6}_{-7}\left(t+6\right)t^{2019}dt=\int\limits^{-6}_{-7}\left(t^{2020}+6t^{2019}\right)dt\)
\(=\left(\dfrac{t^{2021}}{2021}+\dfrac{3t^{2020}}{1010}\right)|^{-6}_{-7}=\dfrac{7^{2021}-6^{2021}}{2021}-\dfrac{3}{1010}\left(7^{2020}-6^{2020}\right)\)
E cảm ơn ạ.