K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 4 2022
\(I=\int\limits^{\dfrac{\pi}{2}}_0\left(1+cosx+x.cosx\right)e^{sinx}dx=\int\limits^{\dfrac{\pi}{2}}_0e^{sinx}dx+\int\limits^{\dfrac{\pi}{2}}_0\left(x+1\right).cosx.e^{sinx}dx=I_1+I_2\)
Xét \(I_2\), đặt \(\left\{{}\begin{matrix}u=x+1\\dv=cosx.e^{sinx}dx\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}du=dx\\v=e^{sinx}\end{matrix}\right.\)
\(\Rightarrow I_2=\left(x+1\right).e^{sinx}|^{\dfrac{\pi}{2}}_0-\int\limits^{\dfrac{\pi}{2}}_0e^{sinx}dx=\left(\dfrac{\pi}{2}+1\right)e-1-I_1\)
\(\Rightarrow I=I_1+\left(\dfrac{\pi}{2}+1\right)e-1-I_1=\left(\dfrac{\pi}{2}+1\right)e-1\)
NV
Nguyễn Việt Lâm
Giáo viên
11 tháng 12 2021
Đề bài sai, góc giữa SC và (SAB) luôn nhỏ hơn 45 độ
Nếu góc lớn hơn 45 độ (như đề bài là góc 60 độ) thì độ dài SA sẽ tính ra 1 số âm!
TD
1
25 tháng 12 2016
đặt \(x=\frac{\sqrt{3}}{cost};\forall t\in\left(0;\frac{\pi}{2}\right)\Rightarrow tant>0\)
\(dx=d\left(\frac{\sqrt{3}}{cost}\right)=\frac{-\sqrt{3}sint}{cos^2t}dt\)
Thay vào, ta có \(\int\frac{\sqrt{3}\cdot\frac{-\sqrt{3}sint}{cos^2t}}{\frac{\sqrt{3}}{cost}\sqrt{\frac{3}{cos^2t}-3}}dt=\int\frac{-3\cdot\frac{sint}{cos^2t}}{\frac{3}{cost}\cdot\sqrt{tan^2t}}dt=\int\frac{-sint}{cost\cdot tant}dt=-\int dt=-t+C\)
Bây giờ thay t vào là ra
NV
Nguyễn Việt Lâm
Giáo viên
8 tháng 2 2022
\(\int\left(\dfrac{7}{cos^2x}+cosx-3^x+2\right)dx=7tanx+sinx-\dfrac{3^x}{ln3}+2x+C\)
NT
1
HT
29 tháng 12 2020
Lâu ko ôn lại cũng hơi miss tích phân r :v
\(\int\limits^{\dfrac{-\pi}{4}}_{\dfrac{\pi}{4}}\tan x.dx\)
\(\int\tan x.dx=\int\dfrac{\sin x}{\cos x}.dx=-\int\dfrac{1}{\cos x}.d\left(\cos x\right)=-ln\left|\cos x\right|\)
\(\Rightarrow\int\limits^{\dfrac{-\pi}{4}}_{\dfrac{\pi}{4}}\tan x.dx=-ln\left|\cos\dfrac{-\pi}{4}\right|+ln\left|\cos\dfrac{\pi}{4}\right|\)
10
1
AH
Akai Haruma
Giáo viên
2 tháng 2 2023
Lời giải:
\(\int ^{\frac{\pi}{2}}_{0}\frac{\sin 2x\cos x}{1+\cos x}dx=\int ^{\frac{\pi}{2}}_{0}\frac{2\sin x\cos ^2x}{\cos x+1}dx=2\int ^{\frac{\pi}{2}}_{0}\frac{\cos^2x\sin xdx}{\cos x+1}\)
\(=2\int ^{\frac{\pi}{2}}_{0}\frac{-\cos ^2xd(\cos x)}{\cos x+1}=2\int ^{0}_{1}\frac{-t^2dt}{t+1}=2\int ^{1}_{0}\frac{t^2}{t+1}dt\)
\(=2\int^1_0\frac{(t^2-1)+1}{t+1}dt=2\int ^1_0(t-1+\frac{1}{t+1})dt\)
\(=2(\frac{t^2}{2}-t+\ln|t+1|)|^{1}_0=2\ln 2-1\)
LT
0
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 6 2021
- Với \(x=2\) chuỗi hiển nhiên hội tụ
- Với \(x\ne2\):
\(u_{n+1}=\dfrac{\left(-1\right)^{n+1}\left(x-2\right)^{2n+2}}{\left(n^2+2n+2\right)4^{n+1}}\)
\(\lim\limits\left|\dfrac{u_{n+1}}{u_n}\right|=\lim\left|\dfrac{\left(-1\right)^{n+1}.\left(x-2\right)^{2n+2}}{\left(n^2+2n+2\right).4^{n+1}}.\dfrac{\left(n^2+1\right)4^n}{\left(-1\right)^n.\left(x-2\right)^{2n}}\right|\)
\(=\left|\dfrac{\left(x-2\right)^2}{4}\right|< 1\)
\(\Rightarrow-2< x-2< 2\Rightarrow0< x< 4\)
- Với \(x=4\) chuỗi trở thành: \(\sum\limits^{\infty}_{n=1}\dfrac{\left(-1\right)^n.2^{2n}}{\left(n^2+1\right).4^n}=\sum\limits^{\infty}_{n=1}\dfrac{\left(-1\right)^n}{n^2+1}\) hội tụ theo tiêu chuẩn Leibniz
- Với \(x=0\) chuổi trở thành \(\sum\limits^{\infty}_{n=1}\dfrac{\left(-1\right)^n}{n^2+1}\) giống như trên hội tụ theo t/c Leibniz
Vậy miền hội tụ của chuỗi là \(x\in\left[0;4\right]\)
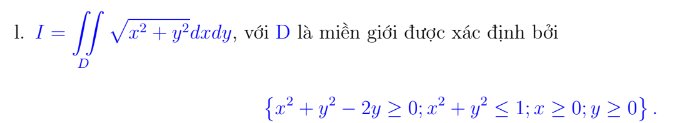
Giao điểm của 2 pt đường tròn \(\left(\dfrac{\sqrt{3}}{2};\dfrac{1}{2}\right)\)
\(\left\{{}\begin{matrix}x=r\cos\varphi\\y=r\sin\varphi\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}r\in\left[2\sin\varphi;1\right]\\\varphi\in\left[0;\dfrac{\pi}{6}\right]\\\left|J\right|=r\end{matrix}\right.\)
\(\Rightarrow I=\int\limits^{\dfrac{\pi}{6}}_0d\varphi\int\limits^1_{2\sin\varphi}\sqrt{r^2}.rdr=\int\limits^{\dfrac{\pi}{6}}_0d\varphi\int\limits^1_{2\sin\varphi}r^2dr=\dfrac{1}{3}\int\limits^{\dfrac{\pi}{6}}_0\left(1-8\sin^3\varphi\right)d\varphi=...\)