Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Khi a = 1dm:
Diện tích một mặt `(S) = a^2 = 1^2 = 1dm^2`
Thể tích `(V) = a^3 = 1^3 = 1dm^3`
Khi a = 3dm:
Diện tích một mặt `(S) = a^2 = 3^2 = 9dm^2`
Thể tích `(V) = a^3 = 3^3 = 27dm^3`
b) Để S = `25dm^2`, ta cần tìm giá trị của a. Ta có:
`a^2 = 25`
=> `a = √25 = 5dm`
c) Để V = `64dm^3`, ta cần tìm giá trị của a. Ta có:
`a^3 = 64`
=> `a = ∛64 = 4dm`

Đáp án A
Giả sử cạnh của hình lập phương là a. Khi đó AB' = x
2
. Xét tam giác vuông AB’C’ vuông tại B’ ta có ![]()
![]() .
.
Do đó ![]()
![]()

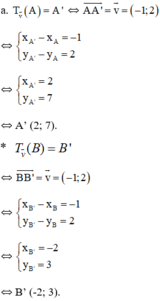
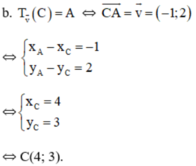
c) Đường thẳng d có vecto pháp tuyến là n→(1;-2) nên 1 vecto chỉ phương của d là(2; 1)
=> Vecto v→ không cùng phương với vecto chỉ phương của đường thẳng d
=> Qua phép tịnh tiến v→ biến đường thẳng d thành đường thẳng d’ song song với d.
Nên đường thẳng d’ có dạng : x- 2y + m= 0
Lại có B(-1; 1) d nên B’(-2;3) d’
Thay tọa độ điểm B’ vào phương trình d’ ta được:
-2 -2.3 +m =0 ⇔ m= 8
Vậy phương trình đường thẳng d’ là:x- 2y + 8 = 0

Chọn B.
Lời giải.
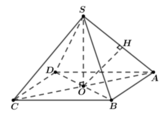
Xét hình chóp tứ giác đều S.ABCD, đặt AB =x, SO =h. Với O là tâm của hình vuông ABCD ⇒ S O ⊥ ( A B C D ) . Qua O kẻ đường thẳng OH vuông góc với SA với H ∈ SA
Ta có
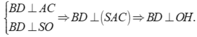
Suy ra OH là đoạn vuông góc chung của SA và BD
Theo bài ra, ta có
![]()
Tam giác SAO vuông tại O, có đường cao OH suy ra
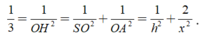
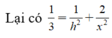
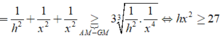
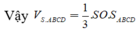
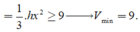

ΔABC vuông tại B
=>\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
ΔA'AC vuông tại A
=>\(A'C=\sqrt{A'A^2+AC^2}=a\sqrt{3}\)
=>Độ dài đường chéo là \(a\sqrt{3}\)

Bài 1:
Số cách đi: \(6.4.\left(6-1\right).\left(4-1\right)=360\)
Bài 2: Gọi số đó là \(\overline{abcd}\)
Số cách lập 4 chữ số lẻ bất kì: d có 3 cách chọn, a có 4, b có 4, c có 3 \(\Rightarrow3.4.4.3=144\) số
Số cách lập số lẻ ko có mặt số 3: d có 2 cách, a có 3 cách, b có 3 cách, c có 2 cách \(\Rightarrow2.3.3.2=36\) số
\(\Rightarrow\) Có \(144-36=108\) số thỏa mãn



Đáp án A