OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tham gia cuộc thi "Nhà giáo sáng tạo" ẫm giải thưởng với tổng giá trị lên đến 10 triệu VNĐ

Mini game 20/11 tri ân thầy cô, nhận thưởng hấp dẫn - Tham gia ngay!

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
19 tháng 4 2018

Cho tứ diện S.ABC có các cạnh SA,SB,SC đôi một vuông góc với nhau. Biết SA = 3a, SB = 4a, SC = 5a. Tính theo a thể tích V của khối tứ diện S.ABC

A. V = 20 a 3

B. V = 10 a 3

C.  5 a 3 2

D. 5 a 3

#Toán lớp 12
1
CM
Cao Minh Tâm
19 tháng 4 2018

Chọn B

Có 

Đúng(0)
PT
Pham Trong Bach
18 tháng 1 2019
Cho khối chóp tam giác S.ABC có SA = 3, SB = 4, SC = 5 và SA, SB, SC đôi một vuông góc. Khối cầu ngoại tiếp tứ diện S.ABC có thể tích là: A. 25 2 π B.  125 2 π 3 C. 10 2 π 3 D. 5 2 π 3 3 ...
Đọc tiếp

Cho khối chóp tam giác S.ABC có SA = 3, SB = 4, SC = 5 và SA, SB, SC đôi một vuông góc. Khối cầu ngoại tiếp tứ diện S.ABC có thể tích là:

A. 25 2 π

B.  125 2 π 3

C. 10 2 π 3

D. 5 2 π 3 3

#Toán lớp 12
1
CM
Cao Minh Tâm
18 tháng 1 2019

Đáp án B

Gọi M,N lần lượt là trung điểm SC, AB

Vì ΔSAB vuông góc tại S nên N là tâm đường tròn ngoại tiếp ΔSAB .

Trong mặt phẳng (MSN) dựng hình chữ nhật MSNO thì ON là trục đường tròn ngoại tiếp ΔSAB và OM là đường trung trực của đoạn SC trong mặt phẳng (OSC)

Đúng(0)
PT
Pham Trong Bach
20 tháng 1 2018
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại đỉnh B, AB = a, SA = 2a và SA vuông góc với mặt phẳng đáy. Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích khối tứ diện S.AHK. A. V = 4 a 3 15 B.  V = 8 a 3 45 C.  V = 8 a 3 15 D. V = 4 a 3 5 ...
Đọc tiếp

Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại đỉnh B, AB = a, SA = 2a và SA vuông góc với mặt phẳng đáy. Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB, SC. Tính thể tích khối tứ diện S.AHK.

A. V = 4 a 3 15

B.  V = 8 a 3 45

C.  V = 8 a 3 15

D. V = 4 a 3 5

#Toán lớp 12
1
CM
Cao Minh Tâm
20 tháng 1 2018

Đúng(0)
PT
Pham Trong Bach
18 tháng 11 2019
Cho khối chóp S.ABC có A S B ⏜ = B S C ⏜ = C S A ⏜ = 60 0 , SA=a, SB=2a, SC=4a. Tính thể tích khối chóp S.ABC theo a   ...
Đọc tiếp

Cho khối chóp S.ABC có A S B ⏜ = B S C ⏜ = C S A ⏜ = 60 0 , SA=a, SB=2a, SC=4a. Tính thể tích khối chóp S.ABC theo a

 
#Toán lớp 12
1
CM
Cao Minh Tâm
18 tháng 11 2019

Đúng(0)
PT
Pham Trong Bach
30 tháng 3 2018

Cho khối chóp S.ABC có SA, SB, SC đôi một vuông góc với nhau và SA = a, SB = b, SC = c. Tính thể tích khối chóp S.ABC.

A.  V = 1 6 a b c

B. V = 1 3 a b c

C. V = a b c

D. V = 1 2 a b c

#Toán lớp 12
1
CM
Cao Minh Tâm
30 tháng 3 2018

Đáp án A

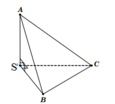
Phương pháp:

 

Thể tích khối chóp vuông

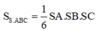
Cách giải:

S.ABC có SA, SB, SC đôi một vuông góc với nhau

⇒ S.ABC là tứ diện vuông tại đỉnh S

Đúng(0)
PT
Pham Trong Bach
6 tháng 1 2018
Cho khối chóp S . A B C có S A ,   S B ,   S C đôi một vuông góc với nhau và  S A = a ,   S B = b ,   S C = c . Tính thể tích khối chóp  S . A B C . ...
Đọc tiếp

Cho khối chóp S . A B C có S A ,   S B ,   S C đôi một vuông góc với nhau và  S A = a ,   S B = b ,   S C = c . Tính thể tích khối chóp  S . A B C .
#Toán lớp 12
1
CM
Cao Minh Tâm
6 tháng 1 2018

Đáp án A

Đúng(0)
PT
Pham Trong Bach
27 tháng 5 2018
Cho hình chóp S.ABC có các cạnh SA = A, SB = 2, SC = 3, AB = 3 , BC = CA = 7 . Tính thể tích V khối chóp S.ABC. A. V = 2 4 B.  V = 3 2 C. V = 2 2 D. V = 3 4 ...
Đọc tiếp

Cho hình chóp S.ABC có các cạnh SA = A, SB = 2, SC = 3, AB = 3 , BC = CA = 7 . Tính thể tích V khối chóp S.ABC.

A. V = 2 4

B.  V = 3 2

C. V = 2 2

D. V = 3 4

#Toán lớp 12
1
CM
Cao Minh Tâm
27 tháng 5 2018

Đáp án C

Đúng(0)
PT
Pham Trong Bach
4 tháng 1 2019
Cho khối chóp S.ABC có SA=a, SB=2a, SC=3a. Thể tích lớn nhất của khối chóp là ...
Đọc tiếp

Cho khối chóp S.ABC có SA=a, SB=2a, SC=3a. Thể tích lớn nhất của khối chóp là
#Toán lớp 12
1
CM
Cao Minh Tâm
4 tháng 1 2019

Chọn D

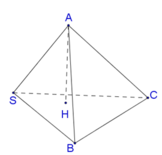
Gọi H là hình chiếu của S lên mặt phẳng (ABC).

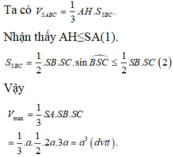
Dấu “=” xảy ra khi SA,SB,SC vuông góc với nhau từng đôi một.

Đúng(0)
PT
Pham Trong Bach
31 tháng 3 2019
Cho khối chóp S.ABC có SA = a 2 , SB = 2a, SC = 2 2 a và ASB = BSC = CSA = 60 ° . Tính thể tích của khối chóp đã cho. A.  4 3 a 3 B. 2 3 3 a 3 C. 2 a 3 D. 2 2 3 a 3 ...
Đọc tiếp

Cho khối chóp S.ABC có SA = a 2 , SB = 2a, SC = 2 2 a và ASB = BSC = CSA = 60 ° . Tính thể tích của khối chóp đã cho.

A.  4 3 a 3

B. 2 3 3 a 3

C. 2 a 3

D. 2 2 3 a 3

#Toán lớp 12
1
CM
Cao Minh Tâm
31 tháng 3 2019

Chọn D.

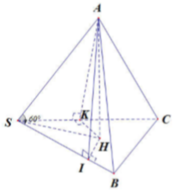
Gọi là hình chiếu vuông góc của A lên mp (SBC) . Gọi I, K lần lượt là hình chiếu vuông góc của H lên SB và SC.

Ta có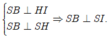 

Chứng minh tương tự ta được SC ⊥ SK

∆ SAI =  ∆ SAK  (cạnh huyền – góc nhọn) => SI = SK

Khi đó  ∆ SHI = ∆ SHK  (cạnh huyền – cạnh góc vuông) => HI = HK. Do đó SH là đường phan giác trong của BSC, nên HSI = 30 °

Trong tam giác vuông SAI, 

Trong tam giác vuông HIS, 

Khi đó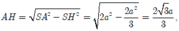 

Vậy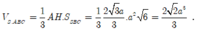 

Cách 2: Sử dụng công thức tính nhanh

Nếu khối chóp S.ABC có 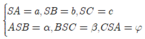 thì 

Áp dụng: Với 

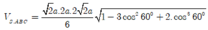
Cách 3:

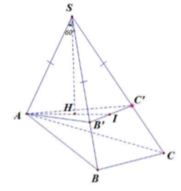
Trên các cạnh SB, SC lần lượt lấy các điểm B’, C’ sao cho SB' = SC' = SA = a 2

Khi đó chóp S.AB'C' là khối chóp tam giác đều. Đồng thời ASB = BSC = CSA = 60 °  nên AB' = B'C' = AC' = SA = a 2

Gọi H là hình chiếu của S lên mặt phẳng (AB'C'). Khi đó dễ dàng chứng minh được các tam giác SHA, SHB', SHC' bằng nhau. Suy ra HA, HB', HC' bằng nhau. Hay H là tâm đường tròn ngoại tiếp tam giác AB'C'. Vì tam giác AB'C' đều nên H cũng là trọng tâm tam giác AB'C'.

Ta có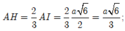 

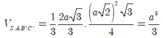
Ta có

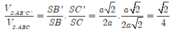
Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP