PD
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CH
Cô Hoàng Huyền
Admin
VIP
4 tháng 12 2017
a) Xét tam giác cân OCD có OH là đường cao nên đồng thời là trung tuyến. Vậy thì HC = HD.
Xét tứ giác ODBC có hai đường chéo cắt nhau tại trung điểm mỗi đường nên nó là hình bình hành.
Lại có hai đường chéo OB và CD vuông góc với nhau nên ODBC là hình thoi.
b) Do ODBC là hình thoi nên OC = CB.
Xét tam giác OBC có OB = OC = BC ( = R) nên OBC là tam giác đều. Vậy thì \(\widehat{OBC}=60^o\)
c) Xét tam giác OCM có CB là đường trung tuyến ứng với cạnh OM.
Lại có \(CB=\frac{1}{2}OM\) nên tam giác OCM vuông tại C.
Từ đó suy ra MC là tiếp tuyến tại C của đường tròn (O)
d) Xét tam giác vuông OCM có CH là đường cao nên áp dụng hệ thức lượng trong tam giác vuông, ta có:
\(CH^2=OH.HM=HB.HM\)
Tam giác OCI vuông tại C có OH là đường cao nên ta có:
\(OH^2=HI.HC=HI.HD\)
Vậy nên \(HI.HD+HB.HM=OH^2+CH^2=OC^2=R^2\)
Vậy \(HI.HD+HB.HM=R^2\)
CL
0
17 tháng 4 2017
iải:
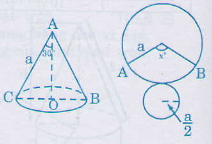
Theo đề bài: góc ở đỉnh cả hình nón là 600 nên suy ra đường kính của đường tròn đáy của một hình nón bằng a(do ∆ABC đều). Vậy bán kính đáy của hình nón là
Đường sinh của hình nón là a.
Độ dài cung hình quạt n0, bán kính a bằng chu vi đáy là a.
Độ dài cung hình quạt trong n0, bán kính a bằng chu vi đáy hình tròn nên ta có:
Suy ra n0 = 1800.
8 tháng 2 2021
a) Xét tứ giác BIEM có
\(\widehat{IBM}\) và \(\widehat{IEM}\) là hai góc đối
\(\widehat{IBM}+\widehat{IEM}=180^0\)(\(90^0+90^0=180^0\))
Do đó: BIEM là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
⇔B,I,E,M cùng thuộc 1 đường tròn(đpcm)
b) Ta có: ABCD là hình vuông(gt)
nên BD là tia phân giác của \(\widehat{ABC}\)(Định lí hình vuông)
⇔BE là tia phân giác của \(\widehat{ABC}\)
⇔\(\widehat{ABD}=\dfrac{\widehat{ABC}}{2}=\dfrac{90^0}{2}=45^0\)
hay \(\widehat{IBE}=45^0\)
Ta có: BIEM là tứ giác nội tiếp(cmt)
nên \(\widehat{IBE}=\widehat{IME}\)(Định lí)
mà \(\widehat{IBE}=45^0\)(cmt)
nên \(\widehat{IME}=45^0\)
Vậy: \(\widehat{IME}=45^0\)