
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

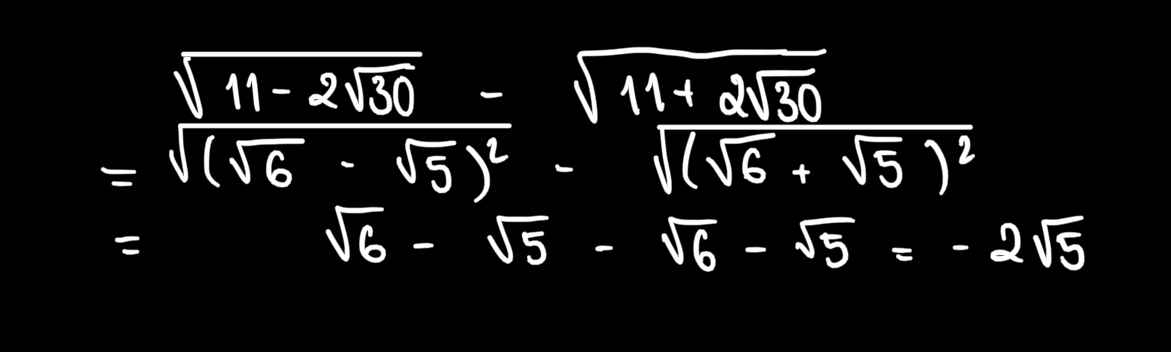

Đặt \(A=\sqrt{11-2\sqrt{30}}-\sqrt{11+2\sqrt{30}}\)
\(\Leftrightarrow A^2=11-2\sqrt{30}+11+2\sqrt{30}-2\sqrt{\left(11-2\sqrt{30}\right)\left(11+2\sqrt{30}\right)}\)
\(\Leftrightarrow A^2=22-2\sqrt{11^2-\left(2\sqrt{30}\right)^2}\)
\(\Leftrightarrow A^2=22-2=20\)
\(\Leftrightarrow A=\pm\sqrt{20}\)
Vì \(\sqrt{11-2\sqrt{30}}< \sqrt{11+2\sqrt{30}}\)
Nên A chỉ nhận giá trị \(-\sqrt{20}\)

\(D=\sqrt{6-2.\sqrt{5}.\sqrt{6}+5}-\sqrt{6+2.\sqrt{5}.\sqrt{6}+5}\)
\(D=\sqrt{\left(\sqrt{6}-\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{6}+\sqrt{5}\right)^2}\)
\(D=|\sqrt{6}-\sqrt{5}|-|\sqrt{6}+\sqrt{5}|\)
\(D=\sqrt{6}-\sqrt{5}-\sqrt{6}-\sqrt{5}\)
\(D=-2\sqrt{5}\)

\(\sqrt{11-2\sqrt{30}}-\sqrt{11+2\sqrt{30}}\)
\(=\sqrt{\left(\sqrt{6}-\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{6}+\sqrt{5}\right)^2}\)
\(=\sqrt{6}-\sqrt{5}-\sqrt{6}-\sqrt{5}\)
\(=-2\sqrt{5}\)

\(A=\dfrac{\sqrt{3}-3}{\sqrt{2-\sqrt{3}}+2\sqrt{2}}+\dfrac{\sqrt{3}+3}{\sqrt{2+\sqrt{3}}-2\sqrt{2}}\)
\(A=\dfrac{\sqrt{2}\left(\sqrt{3}-3\right)}{\sqrt{2}.\left(\sqrt{2-\sqrt{3}}+2\sqrt{2}\right)}+\dfrac{\sqrt{2}.\left(\sqrt{3}+3\right)}{\sqrt{2}.\left(\sqrt{2+\sqrt{3}}-2\sqrt{2}\right)}\)
\(A=\dfrac{\sqrt{6}-3\sqrt{2}}{\sqrt{4-2\sqrt{3}}+4}+\dfrac{\sqrt{6}+3\sqrt{2}}{\sqrt{4+2\sqrt{3}}-4}\)
\(A=\dfrac{\sqrt{6}-3\sqrt{2}}{\sqrt{\left(\sqrt{3}-1\right)^2}+4}+\dfrac{\sqrt{6}+3\sqrt{2}}{\sqrt{\left(\sqrt{3}+1\right)^2}-4}\)
\(A=\dfrac{\sqrt{6}-3\sqrt{2}}{\sqrt{3}-1+4}+\dfrac{\sqrt{6}+3\sqrt{2}}{\sqrt{3}+1-4}\)
\(A=\dfrac{\sqrt{3}\left(\sqrt{2}-\sqrt{6}\right)}{\sqrt{3}\left(1+\sqrt{3}\right)}+\dfrac{\sqrt{3}\left(\sqrt{2}+\sqrt{6}\right)}{\sqrt{3}\left(1-\sqrt{3}\right)}\)
\(A=\dfrac{\sqrt{2}-\sqrt{6}}{1+\sqrt{3}}+\dfrac{\sqrt{2}+\sqrt{6}}{1-\sqrt{3}}=\dfrac{\left(\sqrt{2}-\sqrt{6}\right)\left(1-\sqrt{3}\right)+\left(\sqrt{2}+\sqrt{6}\right)\left(1+\sqrt{3}\right)}{\left(1+\sqrt{3}\right)\left(1-\sqrt{3}\right)}\)
\(A=\dfrac{\sqrt{2}-\sqrt{6}-\sqrt{6}+3\sqrt{2}+\sqrt{2}+\sqrt{6}+\sqrt{6}+3\sqrt{2}}{1-3}=\dfrac{8\sqrt{2}}{-2}=-4\sqrt{2}\)
* \(B=\dfrac{\sqrt{11+2\sqrt{30}}-\sqrt{11-2\sqrt{30}}}{\sqrt{5}}\) \(=\dfrac{\sqrt{6+2.\sqrt{6}.\sqrt{5}+5}-\sqrt{6-2.\sqrt{6}.\sqrt{5}+5}}{\sqrt{5}}\)\(=\dfrac{\sqrt{\left(\sqrt{6}+\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{6}-\sqrt{5}\right)^2}}{\sqrt{5}}\)
\(=\dfrac{\sqrt{6}+\sqrt{5}-\sqrt{6}+\sqrt{5}}{\sqrt{5}}=\dfrac{2\sqrt{5}}{\sqrt{5}}=2\)
* \(C=2\sqrt{3+\sqrt{5}}-\left(\sqrt{4+\sqrt{15}}+\sqrt{4-\sqrt{15}}\right)\)
Đặt:\(y=\sqrt{4+\sqrt{15}}+\sqrt{4-\sqrt{15}}\Rightarrow y^2=4+\sqrt{15}+4-\sqrt{15}+2\sqrt{\left(4+\sqrt{15}\right)\left(4-\sqrt{15}\right)}=8+2=10\Rightarrow y=\sqrt{10}\)
Suy ra: \(C=\sqrt{12+4\sqrt{5}}-y=\sqrt{\left(\sqrt{10}+\sqrt{2}\right)^2}-\sqrt{10}=\sqrt{10}+\sqrt{2}-\sqrt{10}=\sqrt{2}\)* \(D=\sqrt{\dfrac{2+\sqrt{3}}{2-\sqrt{3}}}+\sqrt{\dfrac{2-\sqrt{3}}{2+\sqrt{3}}}=\dfrac{\left(\sqrt{2+\sqrt{3}}\right)\left(\sqrt{2+\sqrt{3}}\right)+\left(\sqrt{2-\sqrt{3}}\right)\left(\sqrt{2-\sqrt{3}}\right)}{\left(\sqrt{2-\sqrt{3}}\right)\left(\sqrt{2+\sqrt{3}}\right)}=\dfrac{2+\sqrt{3}+2-\sqrt{3}}{1}=4\)

\(A=\left(\sqrt{22}+7\sqrt{2}\right)\sqrt{30-7\sqrt{11}}\)
\(2A=\left(\sqrt{44}+7\sqrt{4}\right)\sqrt{60-2.7\sqrt{11}}\)
\(2A=\left(2\sqrt{11}+14\right)\sqrt{7^2-2.7\sqrt{11}+\left(\sqrt{11}\right)^2}\)
\(2A=\left(2\sqrt{11}+14\right)\sqrt{\left(7-\sqrt{11}\right)^2}\)
\(2A=\left(2\sqrt{11}+14\right)\left|7-\sqrt{11}\right|\)
\(2A=\left(2\sqrt{11}+14\right)\left(7-\sqrt{11}\right)\)
\(A=\left(7+\sqrt{11}\right)\left(7-\sqrt{11}\right)\)
\(A=49-11=38\)

tớ ko chép lại đề, kí hiệu nhé
(1) \(=\left(\sqrt{6}-\sqrt{5}\right)^2-\sqrt{\left|\sqrt{6}+\sqrt{5}\right|^2}=\left(\sqrt{6}-\sqrt{5}\right)^2-\left(\sqrt{6}+\sqrt{5}\right)=1-2\sqrt{30}-\sqrt{6}-\sqrt{5}\)
ai ra đề mà để đáp án dài thế này mất thẩm mĩ quá!!!
(2) \(=\sqrt{\left|\sqrt{5}+\sqrt{3}\right|^2}-\sqrt{\left|\sqrt{5}-\sqrt{3}\right|^2}=\left(\sqrt{5}+\sqrt{3}\right)-\left(\sqrt{5}-\sqrt{3}\right)=2\sqrt{3}\)
(3) \(=\sqrt{\left|\sqrt{7}+2\right|^2}-\sqrt{\left|3-\sqrt{5}\right|^2}=\sqrt{7}+2-3+\sqrt{5}=\sqrt{7}+\sqrt{5}-1\)
lại thêm 1 phép tính không đẹp....
(4) \(=\sqrt{\left|3\sqrt{2}-2\right|^2}-\sqrt{\left|3\sqrt{2}+1\right|^2}=3\sqrt{2}-2-3\sqrt{2}-1=-3\)
(5) \(=\sqrt{\left|2\sqrt{3}-1\right|^2}+\sqrt{\left|2\sqrt{3}-3\right|^2}=2\sqrt{3}-1+2\sqrt{3}-3=4\sqrt{3}-4\)
kiểm tra lại kết quả nhé ^^! Cảm ơn!

\(\sqrt{11+2\sqrt{30}}+\sqrt{9+2\sqrt{20}}=\sqrt{\left(\sqrt{6}+\sqrt{5}\right)^2}+\sqrt{\left(\sqrt{5}+2\right)^2}=\sqrt{6}+\sqrt{5}+\sqrt{5}+2=\sqrt{6}+2\sqrt{5}+2\)
