N
0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
26 tháng 1 2022
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AB}{3}=\dfrac{AC}{4}=\dfrac{AC-AB}{4-3}=3\)
Do đó: AB=9(cm); AC=12(cm)
=>BC=15(cm)
26 tháng 1 2022
\(\dfrac{AB}{AC}=\dfrac{3}{4}\Rightarrow\dfrac{AB}{3}=\dfrac{AC}{4}\)
Đặt AB = 3k ; AC = 4K
Ta có : AC - AB = 4k - 3k = k = 3
=> \(AB=9cm;AC=12cm\)
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=15cm\)
TK
2
25 tháng 9 2021
Vì a; b; c à các góc của tam giác => a + b + c = 1800
Ta có : a=b=2c⇒a2=b2=c1a=b=2c⇒a2=b2=c1
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
a2=b2=c1=a+b+c2+2+1=18005=360a2=b2=c1=a+b+c2+2+1=18005=360
⇒{a=b=72c=36⇒{a=b=72c=36
Vậy....
25 tháng 9 2021
Bạn @๖ACE✪ミ★乙ᑌᑎᗴ⁀ᶦᵈᵒᶫ❄丅ᖇưởᑎǤ❄丅ᗴᗩᗰ❄(❄丅ᗴᗩᗰ❄ᑕᑌ丅ᗴ❄)ঔৣ✞ có thể giúp mình viết kĩ và đầy đủ hơn đc ko bn. Mình ko hiểu khá nhiều chỗ còn dãy tỉ số = nhau thì ok r. Bn giải lại r mk tích cho.
5 tháng 9 2019
Kéo dài MN cắt AC tại F
Ta có: \(\hept{\begin{cases}AB//NF\\AB\perp AC\end{cases}\Rightarrow NF\perp}AC\)
Xét tam giác ACN có:
\(\hept{\begin{cases}NF\perp AC\left(cmt\right)\\AH\perp NC\left(gt\right)\end{cases}}\)
Mà M là giao điểm của NF và AH
\(\Rightarrow M\)là trực tâm của tam giác ACN
\(\Rightarrow EC\perp AN\)( tc )
\(\Rightarrow\widehat{AEC}=90^0\)
\(\Rightarrow\Delta AEC\)vuông tại E
H
17 tháng 11 2021
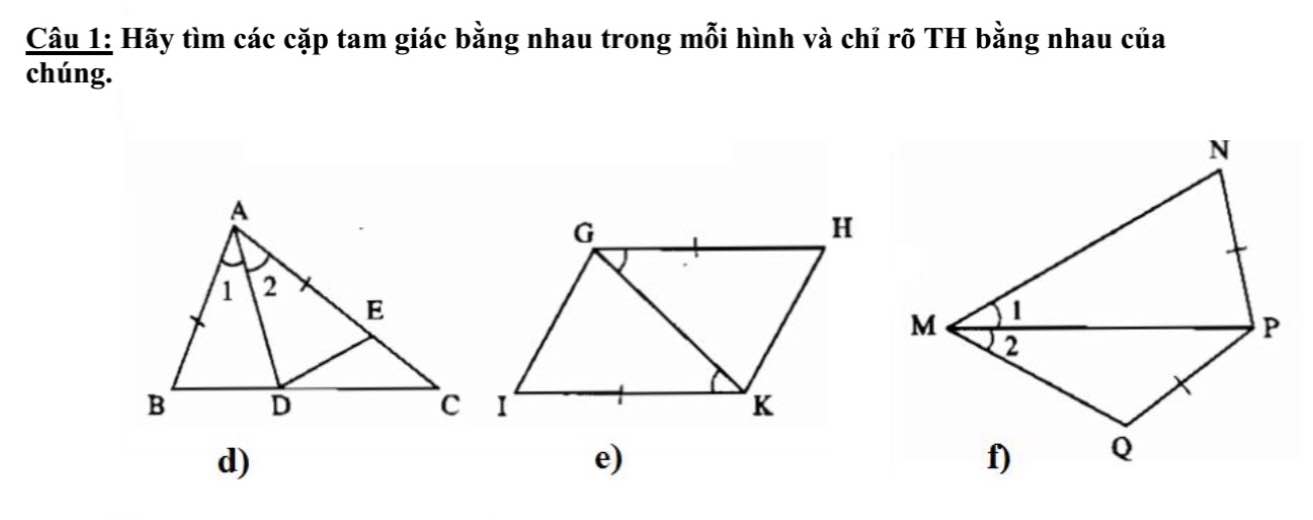
a, Tam giác ABD và tam giác AED ( c-g-c)
b, Tam giác GKI và tam giác HGK ( c-g-c)
c,tam giác QMP và tam giác NMP ( c-g-c)
17 tháng 11 2021
d)△ABD=△AED (c.g.c)
e)△GIK=△KHG (c.g.c)
f)Ko có tam giác bằng nhau vì không có góc xen giữa 2 cạnh bằng nhau
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 12 2021
\(\dfrac{\sqrt{5^2}-\sqrt{19^2}}{\sqrt{8^2}-\sqrt{22^2}}=\dfrac{5-19}{8-22}=\dfrac{-14}{-14}=1\)
DD
Đoàn Đức Hà
Giáo viên
31 tháng 3 2021
\(KB+KC=KB+\left(KA+AC\right)=\left(KB+KA\right)+AC>AB+AC\)
(Theo bất đẳng thức tam giác trong tam giác \(KAB\))