U
5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
CP
1
PN
0
tính nhanh p/s 1+ 5/4 + 5/8 + 5/16 + 5/32 + 5/64
9 tháng 5 2023
b: A=1/3+1/9+...+1/3^10
=>3A=1+1/3+...+1/3^9
=>A*2=1-1/3^10=(3^10-1)/3^10
=>A=(3^10-1)/(2*3^10)
c: C=3/2+3/8+3/32+3/128+3/512
=>4C=6+3/2+...+3/128
=>3C=6-3/512
=>C=1023/512
d: A=1/2+...+1/256
=>2A=1+1/2+...+1/128
=>A=1-1/256=255/256
NQ
2
TD
6 tháng 11 2019
A= 1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256
2A= 2(1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256)
= 1+1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128
=>A = 2A-A =1+1/2 + 1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 -1/2 - 1/4 - 1/8 - 1/16 - 1/32 - 1/64 - 1/128 - 1/256
=1-1/256
=255/256
TH
3
14 tháng 7 2016
1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512
A x 2 = 1/4 ( 1/4 + 1/8 + 1/16 + .......... + 1/512 ) - 1/512
A x 2 = 1/4 - A - 1/512
A x 2 - A = 1/4 - 1/512
A = 1/4 - 1/512
A = 127/512
14 tháng 7 2016
1/4 + 1/8 + 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512
= 1/2 - 1/4 + 1/4 - 1/8 + ... + 1/256 - 1/512
= 1/2 - 1/512
= 255/512
TP
3
1 tháng 8 2016
A = 1/2 + 1/4 + 1/8 + ... + 1/1024
2A = 1 + 1/2 + 1/4 + ... + 1/512
2A - A = (1 + 1/2 + 1/4 + ... + 1/512) - (1/2 + 1/4 + 1/8 + ... + 1/1024)
A = 1 - 1/1024
A = 1023/1024
1 tháng 8 2016
\(A=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+....+\frac{1}{1024}\)
\(\Rightarrow2A=1+\frac{1}{2}+\frac{1}{4}+......+\frac{1}{512}\)
\(\Rightarrow A=2A-A=1-\frac{1}{1024}\)
\(A=\frac{1023}{1024}\)
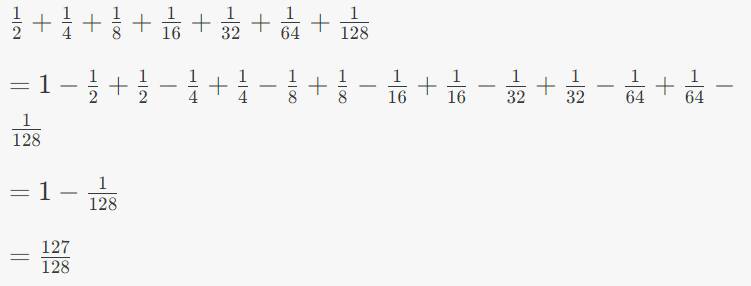
1/2 + 1/4+ 1/8+ 1/16 + 1/32 + 1/64 + 1/128 + 1/256 + 1/512
= 1 – 1/2 + 1/2- 1/4 + 1/4 – 1/8 + 1/8 – 1/16 + 1/16 – 1/32 + 1/32 – 1/64 + 1/64 – 1/128 + 1/128 – 1/256 – 1/256 – 1/512
= 1 – 1/512
= 511/512 .
Câu hỏi của Speed of light - Toán lớp 4 - Học toán với OnlineMath
Em tham khảo bài đc OLM k đúng nhé!