Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(l = R\alpha = 20.\frac{\pi }{{12}} = \frac{{5\pi }}{3}\)
b) \(l = R\alpha = 20.1,5\pi = 30\pi \)
c) Đổi \({35^0} = 35.\frac{\pi }{{180}} = \frac{7\pi }{36}\)
\(l = R\alpha = 20.\frac{7\pi }{36} = \frac{35\pi }{9}\)
d) Đổi \({315^0} = 315.\frac{\pi }{{180}} = \frac{{7\pi }}{4}\)
\(l = R\alpha = 20.\left( {\frac{{7\pi }}{4}} \right) = 35\pi \)

Chọn D
Ta có A=(a-c)2+(b-c)2+(b-d)2-(a-d)2=(a-aq2 )2+(aq-aq2 )2+(aq-aq3)2-(a-aq3)2=0

a.
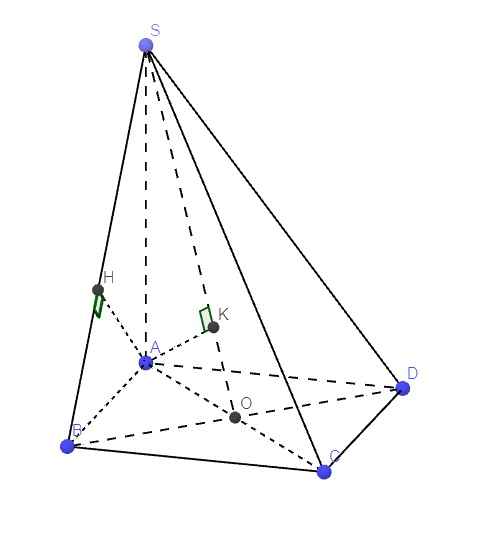
Từ A kẻ \(AH\perp SB\) (1)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\Rightarrow BC\perp AH\) (2)
(1);(2) \(\Rightarrow AH\perp\left(SBC\right)\)
\(\Rightarrow AH=d\left(A;\left(SBC\right)\right)\)
Áp dụng hệ thức lượng trong tam giác vuông SAB:
\(AH=\dfrac{SA.AB}{SB}=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{2a\sqrt{5}}{5}\)
Do \(AD||BC\Rightarrow AD||\left(SBC\right)\Rightarrow d\left(A;\left(SBC\right)\right)=d\left(D;\left(SBC\right)\right)\)
\(\Rightarrow d\left(D;\left(SBC\right)\right)=\dfrac{2a\sqrt{5}}{5}\)
b.
Gọi O là giao điểm 2 đường chéo \(\Rightarrow OA\perp OB\) (t/c hình vuông)
Từ A kẻ \(AK\perp SO\) (1)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp BO\Rightarrow BO\perp\left(SAO\right)\)
\(\Rightarrow BO\perp AK\) (2)
(1);(2) \(\Rightarrow AK\perp\left(SBD\right)\) \(\Rightarrow AK=d\left(A;\left(SBD\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng trong tam giác vuông SAO:
\(AK=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{2a}{3}\)
Do \(\left\{{}\begin{matrix}AC\cap\left(SBD\right)=O\\AO=CO\end{matrix}\right.\) \(\Rightarrow d\left(C;\left(SBD\right)\right)=d\left(A;\left(SBD\right)\right)=\dfrac{2a}{3}\)

a) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{C}}\)
Vậy \(\widehat {BA{\rm{C}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,C} \right]\)
\(AB = BC = AC = a \Rightarrow \Delta ABC\) đều \( \Rightarrow \widehat {BA{\rm{C}}} = \widehat {ABC} = {60^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,C} \right]\) bằng \({60^ \circ }\).
b) \(SA \bot \left( {ABCD} \right) \Rightarrow SA \bot AB,SA \bot A{\rm{D}}\)
Vậy \(\widehat {BA{\rm{D}}}\) là góc phẳng nhị diện của góc nhị diện \(\left[ {B,SA,D} \right]\)
\(ABCD\) là hình thoi \( \Rightarrow \widehat {BA{\rm{D}}} = {180^ \circ } - \widehat {ABC} = {180^ \circ } - {60^ \circ } = {120^ \circ }\)
Vậy số đo của góc nhị diện \(\left[ {B,SA,D} \right]\) bằng \({120^ \circ }\).
c) \(SA \bot \left( {ABCD} \right) \Rightarrow \left( {SC,\left( {ABCD} \right)} \right) = \left( {SC,AC} \right) = \widehat {SCA}\)
\(\Delta SAC\) vuông tại \(A \Rightarrow \tan \widehat {SCA} = \frac{{SA}}{{AC}} = \frac{a}{a} = 1 \Rightarrow \widehat {SCA} = {45^ \circ }\)
Vậy \(\left( {SC,\left( {ABCD} \right)} \right) = {45^ \circ }\).

ghi sai toán olớp 6 nhé ai giúp mình với