Tính nhanh: 45 2 + 33 2...

Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mua vip

Pham Trong Bach

13 tháng 7 2018

Tính nhanh: 45 2 + 33 2 − 22 2 + 90.33

#Hỏi cộng đồng OLM #Toán lớp 8

Cao Minh Tâm

13 tháng 7 2018

Đúng(0)

Các câu hỏi dưới đây có thể giống với câu hỏi trên

tran le thuy duong

19 tháng 10 2018 - olm

45^2+33^2-22^3+90.33

#Hỏi cộng đồng OLM #Toán lớp 8

Ánh Phương

10 tháng 10 2018

Tính nhanh:

45² + 33² - 22² + 90 . 33

#Hỏi cộng đồng OLM #Toán lớp 8

Bùi Quang Sang

10 tháng 10 2018

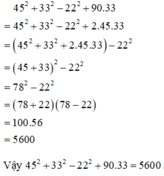
$45^2+33^2-22^2+90.33$

$=\left(45^2+90.33+33^2\right)-22^2$

$=\left(45+33\right)^2-22^2$

$=\left(45+33-22\right).\left(45+33+22\right)$

$=56.100=5600$

Đúng(0)

Ánh Phương

10 tháng 10 2018

Tính nhanh:

45² + 33² - 22² + 90 . 33

#Hỏi cộng đồng OLM #Toán lớp 8

Dũng Nguyễn

10 tháng 10 2018

$45^2+33^2-22^2+90.30$

$=\left(45^2+90.33+33^2\right)-22^2$

$=\left(45^2+2.45.33+33^2\right)-22^2$

$=\left(45+33\right)^2-22^2$

$=\left(45+33-22\right)\left(45+33+22\right)$

$=56.100=5600$

Đúng(0)

Ánh Phương

10 tháng 10 2018

Tính nhanh:

45² + 33² - 22² + 90 . 33

#Hỏi cộng đồng OLM #Toán lớp 8

Bùi Quang Sang

10 tháng 10 2018

$452 + 33 2 - 22 2 + 90.33$

$= (45 2 + 90 . 33 + 33 2) -22 2$

$= (45 + 33) 2 -22 2$

$= (45 + 33 - 22).(45 + 33 + 22)$

$= 56.100$

$= 5600$

Đúng(0)

nhat

15 tháng 11 2019 - olm

tính nhanh (22^2+33^2+46^2+33.44+46.66+46.44):101

#Hỏi cộng đồng OLM #Toán lớp 8

Phạm Đỗ Bảo Ngọc

30 tháng 7 2021 - olm

bài 3; tính nhanh

d, D=40 mũ 2 - 28 mũ 2 + 32 mũ 2+ 80 . 32

e,E=10 . 80, 5 + 10 . 19,5 - 8 . 20,5-8 . 79,5

f,F=50 mũ 2 - 18 mũ 2 + 32 mũ 2 + 100 . 32

g, G= 45 mũ 2 + 33 mũ 2 - 22 mũ 2 + 90 . 33

h, H = 111 mũ 2 - 137 mũ 2 - 48 mũ 2 + 96 . 137

#Hỏi cộng đồng OLM #Toán lớp 8

Nguyễn Thị Thương Hoài

Giáo viên VIP

8 tháng 8 2023

d, D = 40² - 28² + 32² +80.32

D = (40² + 2.40.32 + 32²) - 28²

D = (40 + 32)² - 28²

D = (40 + 32 - 28)(40 + 32 + 28)

D = 44.100

D = 4400

e, E = 10.80,5 + 10.19,5 - 8.20,5 - 8. 79,5

E = 10.(80,5 + 19,5) - 8.( 20,5 + 79,5)

E = 10.100 - 8.100

E = 100.(10-8)

E = 200

Đúng(0)

Nguyễn Thị Thương Hoài

Giáo viên VIP

8 tháng 8 2023

F = 50² - 18² + 32² + 100.32

F = (50² - 18²) + 32.( 32 + 100)

F = (50 -18)(50+18) + 32. 132

F = 32.68 + 32.132

F = 32.( 68 + 132)

F = 32. 200

F = 6400

Đúng(0)

Sách Giáo Khoa

20 tháng 4 2017

Tính nhanh :

a) $37,5.6,5-7,5.3,4-6,6.7,5+3,5.37,5$

b) $45^2+40^2-15^2+80.45$

#Hỏi cộng đồng OLM #Toán lớp 8

Tuyết Nhi Melody

20 tháng 4 2017

Bài giải:

a) 37,5 . 6,5 – 7,5 . 3,4 – 6,6 . 7,5 + 3,5 . 37,5

= (37,5 . 6,5 + 3,5 . 37,5) - (7,5 . 3,4 + 6,6 . 7,5)

= 37,5(6,5 + 3,5) - 7,5(3,4 + 6,6)

= 37,5 . 10 - 7,5 . 10

= 375 - 75 = 300.

b) 45² + 40² – 15²+ 80 . 45 = 45² +2 . 40 . 45 + 40² – 15²

= (40 + 45)² – 15² = 85² – 15² = (85 – 15)(85 + 15) = 70 . 100 = 7000.

Đúng(0)

Nguyễn Nhật Nam

22 tháng 8 2017

a) 37,5.6,5-7,5.3,4-6,6.7,5+3,5.37,5

=(37,5.6,5+3,5.37,5)-(7,5.3,4+6,6.7,5)

=37,5.(6,5+3,5)-7,5.(3,4+6,6)

=37,5.10-7,5.10

=375-75

=300

b) 45²+40²-15²+80.45

=45²+2.40.45+40²-15²

=(45+40)²-15²

=(45+40-15).(45+40+15)

= 70.100

=7000

Đúng(0)

Nguyễn Như Ý

31 tháng 7 2016

Bài 1: Tính nhanh giá trị của biểu thức:

A=23$^2$+46.37+37$^2$

B=27$^2$-44.27+22$^2$

Bài 2:Tính GTNN

A=x$^2$-4x+5

#Hỏi cộng đồng OLM #Toán lớp 8

Trần Việt Linh

31 tháng 7 2016

Bài 1:

$A=23^2+46\cdot37+37^2=23^2+2\cdot23\cdot37+37^2=\left(23+37\right)^2=60^2=3600$

$B=27^2-44\cdot27+22^2=27^2-2\cdot27\cdot22+22^2=\left(27-22\right)^2=5^2=25$

Bài 2:

$A=x^2-4x+5=x^2-4x+4+1=\left(x-2\right)^2+1$

Vì: $\left(x-2\right)^2\ge0$ với mọi x

=> $\left(x-2\right)^2+1\ge1$

Vậy GTNN của A là 1 khi x=2

Đúng(0)

phan thị minh anh

31 tháng 7 2016

$A=23^2+2.23.37+37^2=\left(23+37\right)^2=60^2=3600$

$B=27^2-2.27.22+22^2=\left(27-22\right)^2=5^2=25$

$A=x^2-4x+5=\left(x-2\right)^2+1\ge1$

=> A min=1 khi x=2

Đúng(0)

Lê khắc Tuấn Minh

13 tháng 11 2016

Tính nhanh

$\left(50^2+48^2+46^2+....+4^2+2^2\right)-\left(49^2+47^2+45^2+...+5^2+3^2+1^2\right)$

#Hỏi cộng đồng OLM #Toán lớp 8

Nguyễn Đình Dũng

13 tháng 11 2016

(50²+48²+...+2²) - (49²+47²+...+1²)

= (50²-49²) + (48²-47²) + ... + (2²-1²)

= (50+49)(50-49) + (48+47)(48-47) + ... + (2+1)(2-1)

= 50+49+48+47+...+1

= $\frac{\left(50+1\right).50}{2}=\frac{51.50}{2}=1275$

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP