K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
AH
Akai Haruma
Giáo viên
25 tháng 10 2021
Lời giải:
a.
$2x(3x^2-4x+2)=2x.3x^2-2x.4x+2x.2$
$=6x^3-8x^2+4x$
b.
$2x(3x+5)-3(2x^2-2x+3)=2x.3x+2x.5-(3.2x^2-3.2x+3.3)$
$=6x^2+10x-6x^2+6x-9=16x-9$
CM
26 tháng 9 2018
Áp dụng kết quả Bài 31 a) (trang 50 SGK Toán 8 Tập 1) ta được:
30 tháng 8 2016
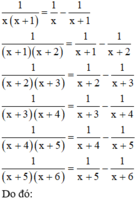
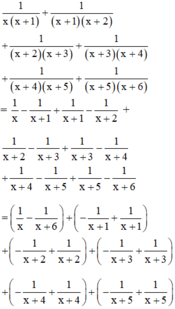
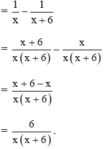
làm khuyến mại 1 câu;
a) = 12x2 -12x2 +20x -10x +17 =0
10x = -17
x = -17/10
MV
0
4 tháng 8 2016
a) (x+2)(x-3)=0
<=> x+2=0
x-3=0
<=> x=-2
x= 3
b) 2x-x2=0
<=> x(2-x) =0
<=> x=0
2-x=0
<=> x=0
x=2
4 tháng 8 2016
a)(x+2)(x-3)=0
=>\(\orbr{\begin{cases}x+2=0\\x-3=0\end{cases}}\)=>\(\orbr{\begin{cases}x=-2\\x=3\end{cases}}\)
Vậy x=-2 hoặc x=3
b) 2x-x2=0
=> x(2-x)=0
=>\(\orbr{\begin{cases}x=0\\2-x=0\end{cases}}\)=>\(\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
Vậy x=0 hoặc x=2
B
1
19 tháng 7 2017
Ta có : x2 + 4x
= x2 + 4x + 4 - 4
= (x + 2)2 - 4
Mà ; (x + 2)2 \(\ge0\forall x\)
Nên : (x + 2)2 - 4 \(\ge-4\forall x\)
Vậy GTNN của biểu thức là -4 khi x = -2