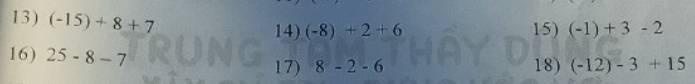Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\frac{1}{40}\)x\(\frac{1}{30}\)x\(\frac{1}{20}\)x\(\frac{1}{12}\)x\(\frac{1}{6}\)x\(\frac{1}{2}\)
= \(\frac{1}{40.30.20.12.6.2}\)
= \(\frac{1}{3456000}\)
k mik nha! (kb nhé!!!)

\(\frac{1}{20}\cdot\frac{1}{30}\cdot\frac{1}{42}\cdot\frac{1}{56}\cdot\frac{1}{72}\cdot\frac{1}{90}\)
\(=\frac{1}{4\cdot5}+\frac{1}{5\cdot6}+\frac{1}{6\cdot7}+\frac{1}{7\cdot8}+\frac{1}{8\cdot9}+\frac{1}{9\cdot10}\)
\(=\frac{1}{4}-\frac{1}{5}+\frac{1}{5}-\frac{1}{6}+\frac{1}{6}-\frac{1}{7}+\frac{1}{7}-\frac{1}{8}+\frac{1}{8}-\frac{1}{9}+\frac{1}{9}-\frac{1}{10}\)
\(=\frac{1}{4}-\frac{1}{10}\)
\(=\frac{6}{40}=\frac{3}{20}\)


Ta có:
A=\(\frac{1}{1.101}+\frac{1}{2.102}+...+\frac{1}{25.125}\)
=\(\frac{1}{100}\left(\frac{100}{1.101}+\frac{100}{2.102}+...+\frac{100}{25.125}\right)\)
=\(\frac{1}{100}\left(1-\frac{1}{101}+\frac{1}{2}-\frac{1}{102}+...+\frac{1}{25}-\frac{1}{125}\right)\)
=\(\frac{1}{100}\left[\left(1+\frac{1}{2}+...+\frac{1}{25}\right)-\left(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{125}\right)\right]\)
B=\(\frac{1}{1.26}+\frac{1}{2.27}+...+\frac{1}{100.125}\)
=\(\frac{1}{25}\left(\frac{25}{1.26}+\frac{25}{2.27}+...+\frac{25}{100.125}\right)\)
=\(\frac{1}{25}\left(1-\frac{1}{26}+\frac{1}{2}-\frac{1}{27}+...+\frac{1}{100}-\frac{1}{125}\right)\)
=\(\frac{1}{25}\left[\left(1+\frac{1}{2}+...+\frac{1}{100}\right)-\left(\frac{1}{26}+\frac{1}{27}+...+\frac{1}{125}\right)\right]\)
=\(\frac{1}{25}\left[\left(1+\frac{1}{2}+...+\frac{1}{25}\right)+\left(\frac{1}{26}+\frac{1}{27}+...+\frac{1}{100}\right)-\left(\frac{1}{26}+\frac{1}{27}+...+\frac{1}{100}\right)-\left(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{125}\right)\right]\)
= \(\frac{1}{25}\left[\left(1+\frac{1}{2}+...+\frac{1}{25}\right)-\left(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{125}\right)\right]\)
=> \(\frac{A}{B}\)=\(\frac{\frac{1}{100}\left[\left(1+\frac{1}{2}+...+\frac{1}{25}\right)-\left(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{125}\right)\right]}{\frac{1}{25}\left[\left(1+\frac{1}{2}+...+\frac{1}{25}\right)-\left(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{125}\right)\right]}\)=\(\frac{1}{\frac{100}{\frac{1}{25}}}\)=\(\frac{1}{100}\cdot25=\frac{25}{100}=\frac{1}{4}\)

Sửa đề: 8666
8666*15+170*4333
=4333*(2*15+170)
=200*4333
=866600

A = 44 . 82 -22 + 18 . 44
= 44 . 82 - 4 + 18 . 44
= 44. ( 82 + 18 ) - 4
= 44 . 100 - 4
= 4400 - 4
= 4396
Ta có: \(A=44\cdot82-2^2+18\cdot44\)
\(=44\cdot\left(82+18\right)-4\)
\(=44\cdot100-4\)
\(=4400-4=4396\)

13: \(\left(-15\right)+8+7\)
\(=\left(-15\right)+\left(8+7\right)\)
=-15+15
=0
14: \(\left(-8\right)+2+6\)
\(=\left(-8\right)+\left(2+6\right)\)
=-8+8
=0
15: \(\left(-1\right)+3-2\)
\(=\left(-1-2\right)+3\)
=-3+3
=0
16: \(25-8-7\)
\(=25-\left(8+7\right)\)
=25-15
=10
17: \(8-2-6\)
\(=8-\left(2+6\right)\)
=8-8
=0
18: \(\left(-12\right)-3+15\)
\(=\left(-12-3\right)+15\)
=-15+15
=0