
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(\int\dfrac{1}{x^3+x^2-22x-40}dx=\int\dfrac{1}{\left(x-5\right)\left(x+2\right)\left(x+4\right)}dx\)
\(=\int\left(\dfrac{1}{63}.\dfrac{1}{x-5}-\dfrac{1}{14}.\dfrac{1}{x+2}+\dfrac{1}{18}.\dfrac{1}{x+4}\right)dx\)
\(=\dfrac{1}{63}ln\left|x-5\right|-\dfrac{1}{14}ln\left|x+2\right|+\dfrac{1}{18}ln\left|x+4\right|+C\)

Chọn C.
Đặt u = G ( x ) d v = f ( x ) d x ⇒ d u = G ( x ) ' d x = g ( x ) d x v = ∫ f ( x ) d x = F ( x )
Suy ra: I = G ( x ) F ( x ) 2 0 - ∫ 0 2 F ( x ) g ( x ) d x
= G(2)F(2) – G(0)F(0) – 3 = 1 – 0 – 3 = -2.

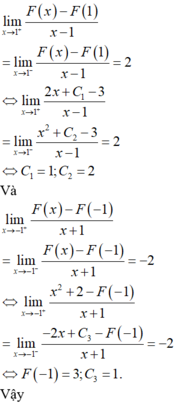
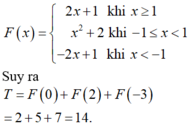
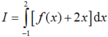
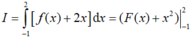
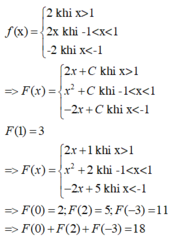
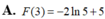
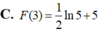
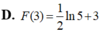
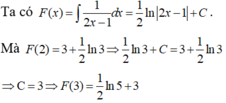
Lời giải:
Ta có:
\(P=\int \frac{x^2-1}{x\sqrt{x^3+x}}dx=\int \frac{\frac{x^2-1}{x^2}}{\frac{\sqrt{x^3+x}}{x}}dx\)
\(=\int \frac{(1-\frac{1}{x^2})dx}{\frac{\sqrt{x^3+x}}{x}}=\int \frac{d\left(x+\frac{1}{x}\right)}{\frac{\sqrt{x^3+x}}{x}}\)
Đặt \(\frac{\sqrt{x^3+x}}{x}=t\Rightarrow t^2=\frac{x^3+x}{x^2}=x+\frac{1}{x}\)
Khi đó: \(P=\int \frac{d(t^2)}{t}=\int \frac{2tdt}{t}=\int 2dt=2t+c=\frac{2\sqrt{x^3+x}}{x}+c\)