Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(=\int\limits^{\dfrac{\pi}{4}}_0\dfrac{3\left(1-cos^2x\right)-4cos^2x}{cos^2x}dx=\int\limits^{\dfrac{\pi}{4}}_0\dfrac{3-7cos^2x}{cos^2x}dx\)
\(=\int\limits^{\dfrac{\pi}{4}}_0\left(\dfrac{3}{cos^2x}-7\right)dx=\left(3tanx-7x\right)|^{\dfrac{\pi}{4}}_0=...\)

\(=\int\limits^{\dfrac{\pi}{4}}_0\dfrac{2cos^2x-1-3\left(1-cos^2x\right)}{cos^2x}dx=\int\limits^{\dfrac{\pi}{4}}_0\dfrac{5cos^2x-4}{cos^2x}dx\)
\(=\int\limits^{\dfrac{\pi}{4}}_0\left(5-\dfrac{4}{cos^2x}\right)dx=\left(5x-4tanx\right)|^{\dfrac{\pi}{4}}_0=...\)

Lần sau bạn lưu ý viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo)
Lời giải:
\(\int ^2_1\frac{x+2}{2x-1}dx=\frac{1}{2}\int ^2_1\frac{2x+4}{2x-1}dx=\frac{1}{2}(\int ^2_1dx+\int ^2_1\frac{5}{2x-1}dx)\)
\(=\frac{1}{2}(\int ^2_1dx+\frac{5}{2}\int ^2_1\frac{d(2x-1)}{2x-1})\)
\(=\frac{1}{2}(|^2_1x+\frac{5}{2}.|^2_1\ln |2x-1|)=\frac{1}{2}(2-1+\frac{5}{2}\ln 3)=\frac{1}{2}+\frac{5}{4}\ln 3\)



Đáp án: B.
Xét f(x) = x 3 + m x 2 + x - 5
Vì 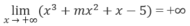
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.